모바일 앱 환경에서는 "latex" 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시길 바랍니다.
오늘은 SGD를 변형한 알고리즘들 중 step size를 모든 파라미터에 동일하게 적용하는 것이 아니라, 각 파라미터별로 조정된 step-size를 적용한 optimizer들을 살펴보자.
loss function은 neural network의 파라미터들로 이루어진 (=매개변수 공간) 공간에서의 함수이고, 이는 매우 고차원의 함수이다. (Neural network의 파라미터 개수가 무수히 많으므로)
모든 파라미터에 대해서 동일한 학습 속도를 적용한다면, 어떤 파라미터들 ( => 그 축의 방향으로) 에 대해서는 크게 이동하지만, 다른 파라미터들 (=> 그 축의 방향으로) 에 대해서는 적게 이동하는 현상들이 발생할 수 있고 이러한 현상을 완화하기 위해서 매개변수마다의 개별적 step-size를 적용해주는 방법들이 나오게 되었다.

가장 유명한 알고리즘들로는 AdaGrad (Adaptive Gradient의 약어), RMSProp (root mean square propagaion의 약어), Adam (Adaptive Momentum의 약어) 등이 있다. 오늘날 가장 많이 쓰이는 것은 Adam 또는 이를 살짝 변형한 알고리즘들이 optimizer로서 가장 많이 쓰인다.
* AdaGrad
$x_{t+1} = x_t - \frac{\eta}{\sqrt{G_t + \epsilon} \odot g_t $ \\
$G_t := \sum_{k=1}^t (g_k)^{\odot 2}$
AdaGrad의 파라미터 업데이트 방식이다.
step-size ($\eta$) 부분에서 $\frac{1}{G_t}$로 scaling된 step-size를 적용한다.
이때, $\epsilon$은 분모가 0이 되는 경우, 0으로 나눠져서 수치 연산에서의 오류가 발생하는 것을 방지하기 위함이다.
$G_t$는 결국 gradient의 (element-wise) 제곱을 의미하는데, gradient는 벡터이므로 여기서의 제곱 연산은 성분별 제곱을 의미한다.
행렬표기로는 다음과 같이 설명할 수 있다.
만약에 neural network에 파라미터가 총 $k$개 있다고 해보자.
그렇다면 (stochastic) gradient $g_t$는 성분이 $k$개인 벡터가 될 것이다. 그 벡터를 외적하였으므로, $G_t$는 $k \times k$ 행렬이 될것이다. 이 중 주 대각성분들을 이용해서 step-size에 대한 scaling을 진행하는 것이다.
AdaGrad는 다음과 같이 적용된다.

gradient의 제곱을 현재 step에서의 gradient만 사용하지 않고, 과거부터 현재까지 누적된 값 ($r_{t+1}$)을 사용해서 step-size scaling을 진행한다.
* RMSProp

RMSProp에서도 동일하게 gradient의 제곱 연산과 square root 연산이 진행되는데 AdaGrad와의 차이점은
여기서는 Exponential moving average이라는 점이다.
즉, $r_{t+1}$도 단순히 과거부터 현재까지 누적된 합을 적용하는 것이 아닌, moving average 연산을 통해 현재 step에서의 gradient 제곱에 더 큰 가중치를 부여하는 방식으로 연산이 진행된다.
여기서 $\beta \in [0, 1)$이고, 경험적으로 $\beta$가 클수록 학습이 더 잘 된다는 것이 알려져 있다.
(예를 들어, 파이토치에서 $\beta$의 Default value는 0.9이다.)
* ADAM
Adam은 gradient에 대해서, 그리고 gradient의 제곱에 대해서 moving average 연산을 수행하여 step-size를 조정한다.
여기서 알 수 있듯이, gradient에 대해서 moving average 연산을 수행하기 때문에 이름에 momentum이 들어가고, step-size를 gradient 제곱에 대해서 scaling해주기 때문에 adaptive라는 이름이 들어가서, Adaptive momentum (Adam)이 된 것이다.

이 때, gradient의 제곱 연산과 square root연산은 RMSProp과 동일하게 'element-wise operation'이다.
그리고 가장 많이 쓰이는 $\beta_1$은 0.9이고, $\beta_2$는 0.999이다. 물론 이는 default 값이고 각자의 모델과 데이터셋에 맞춰 미세하게 조정해주는 (tuning)과정을 거치는 것이 좋다.
또한, 실제 Adam은 $v_{t+1}$, $r_{t+1}$에 대해서 bias-correction이라 하는 보정과정을 거치는데, 위에서는 이를 skip하였다.
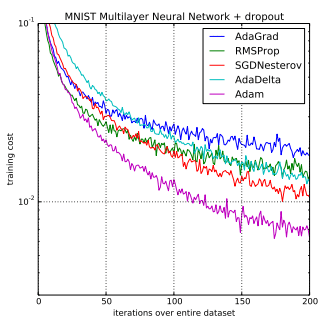
위 그래프를 보면 x축은 epoch이고, y축은 training cost, 즉 loss값이다.
모든 optimizer들에 대해서 전반적으로 loss 값이 잘 감소하지만, Adam이 가장 낮은 loss 값을 기록하면서 또 가장 빨리 떨어짐을 알 수 있다.
특히, Adam 계열의 알고리즘들은 Transformer를 backbone으로 하는 모델 학습에서 SGD, Heavy-ball algorithm보다 더 학습을 잘 시키는 것이 경험적으로 알려져 있는데 이 현상에 대한 이론적인 설명을 시도하는 연구는 지금도 활발하게 진행되고 있다. 이에 대해선 추후 심화 시리즈에서 기회가 된다면 자세하게 알아보자.
자, 그러면 다음과 같은 궁금증이 들 수 있다. 각 파라미터별로 step size를 다르게 적용해주는 방식에서 사용하는 정보는 stochastic gradient의 제곱을 square root에 inverse를 취한 방식이다.
(물론 Adagrad처럼 단순히 누적합을 진행해나가는 방식이 있고, RMSProp/Adam 같은 moving average를 취하는 방식이 있지만, 어찌되었든 제곱의 square root에 inverse를 취한다는 점은 동일하다.)
왜 이러한 방식으로 각 파라미터의 step size를 조정해주는 것일까?
이에 대해선 정답은 없지만 가장 그럴듯한 설명들은 많이 나왔다. 이에 대해서도 추후 심화 시리즈에서 기회가 된다면 자세하게 알아보자.
다음 글에서는 Adam에 대해서 좀 더 자세하게 알아보는 글을 올리고자 한다.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into Optimization: Second-order method - Updated (0) | 2023.04.19 |
|---|---|
| Deep dive into optimization : Adam - Updated (0) | 2023.04.12 |
| Deep dive into Optimization : Momentum(2) - Updated (0) | 2023.04.04 |
| Deep dive into optimization : Momentum (1) - Updated (0) | 2023.03.30 |
| Deep dive into optimization: Gradient descent (3) - Updated (0) | 2023.03.23 |




댓글