"모바일 앱 환경에서는 latex 수식이 깨져 나타나므로 가급적 웹 환경에서 봐주시길 바랍니다."
논문 제목 : Sharpness-Aware Minimization for efficiently improving generalization
출판 연도 : 2021 ICLR (spotlight)
논문 저자 : Pierre Foret et al.
블로그에 올리는 첫 번째 논문에 대한 분석글로 위 논문을 선정하였다.
지난 1년 가까이 학부연구생을 수행하면서 나의 연구주제의 가장 핵심이 되는 알고리즘이었고, 지금도 놓지 못한 알고리즘이다.

<Introduction & Motivation>
위 이미지는 실제 ResNet-56의 loss landscape을 visualization한 이미지이다.
왼쪽의 그림은 상당히 울퉁불퉁한 계곡 모양인데 반해, 오른쪽 그림은 전체적으로 평평한 모양을 하고 있다.
또한 왼쪽의 최소지점을 보면 상당히 뾰족한데 반해, 오른쪽 그림은 왼쪽에 비해 상대적으로 평평한 최소지점을 가지고 있다.
최적화 알고리즘의 목적은 손실 함수를 최소화하는 것이고 이를 우리는 다음과 같이 표현한다.
$\min \mathcal{L}(w) := \sum_{i=1}^n \mathcal{L}_i(w)$
loss function $\mathcal{L}(w)$는 각각의 data sample들의 loss value ($\mathcal{L}_i(w)$)의 합으로 이뤄져 있다.
이때 데이터는 모델이 경험하는 데이터이므로 이를 우리는 Empirical Risk Minimization이라고 부른다.
Empirical risk는 train data에 대해서 모델의 loss 값을 표현하는 용어이고 이를 최소화하는 것이 일반적인 최적화 알고리즘의 목표이다.
그리고 우리는 이때 가장 많이 사용하는 방법이 First-order optimization method이다.
즉, 주어진 파라미터들에 대한 손실함수의 기울기 (gradient)를 이용해서 파라미터를 Negative gradient 방향으로 이동하고, 이는 손실함수의 값을 (= Empirical Risk) 감소시켜 나가게 한다.
하지만 이렇게 해서 우리가 어떤 local minima (넓게는 stationary point)에 도달하였다고 하자.
우리는 오직 손실함수의 1차 미분 정보 (= gradient)만을 활용했기 때문에 2차 미분 정보 (=Curvature)는 없다.
즉, 단순하게 SGD 계열의 알고리즘들만을 활용해서 최적화를 진행하였을 때 Empirical risk는 잘 감소할지 몰라도 모델의 파라미터가 수렴한 local minima가 위 그림에서 왼쪽과 같은 지점일지, 오른쪽과 같은 지점일지는 알 수 없는 것이다.
그렇다면 왼쪽의 local minima가 더 generalization을 잘하는가 아니면 오른쪽의 local minima가 더 generalization을 잘하게 하는가?에 대한 궁금증이 들 것이다.
이에 대해서는 상당히 많은 연구들이 진행되었고, 결과부터 이야기하자면 오른쪽의 local minima, 즉 더 평평한 (= flat) local minima가 더 generalization을 잘한다는 것이 일반적으로 받아들여지고 있는 점이다.
물론, 무조건 그렇다는 것은 아니다. 하지만 local minima의 curvature가 작으면 작을수록 (=More flat), 모델의 일반화 성능이 더 우수하다는, 둘 사이의 높은 상관관계가 존재함이 많은 논문들을 통해 보여졌다.
Sharpness-Aware Minimization은 위와 같은 이전의 연구들에서 영감을 받아 단순하게 Empirical risk만 감소하는 것이 아닌 파라미터의 'Sharpness' ( = curvature)도 함께 감소시켜 나가는 알고리즘을 제안한 논문이다.
<Theoretical Background>
먼저 SAM 저자들은 다음과 같은 inequality를 증명해낸다.
$\mathcal{L}_D(w) \le [\max_{\lVert \epsilon \rVert_2 \le \rho} \mathcal{L}(w + \epsilon) - \mathcal{L}(w)] + h(\lVert w \rVert_2^2 / \rho^2)$
이때 $h$는 어떤 증가함수이다.
위 inequality에서 LHS는 모델의 generalization error ( = Expected risk)를 의미한다.
즉 모델의 generalization error는 RHS로 upper bound된다는 것을 보여주는데 이 부등식은 'PAC-Bayesian generalization bound'를 활용해 유도하였다. 'PAC-Bayesian'에 대해서는 추후 자세하게 다룰 기회가 있을 것이다.
결국 SAM은 위 부등식의 RHS를 최소화하는 알고리즘이다.
즉, 모델의 generalization error가 어떤 upper bound term을 가지고 있는데 이 upper bound term을 최소화하면 결국 모델의 generalization error를 최대한 작아지는 것을 기대할 수 있다는 것이다.
이때 RHS를 자세하게 살펴보면 $\mathcal{L}(w)$는 train loss이고, $\max_{\lVert \epsilon \rVert_2 \le \rho} \mathcal{L}(w + \epsilon) - \mathcal{L}(w)$가 바로 현재 파라미터에서 loss function의 sharpness를 나타내는 항이다.
이 term을 조금 더 자세하게 살펴보자.
우선, $\lVert \epsilon \rVert_2 \le \rho$는 epsilon의 L2-norm이 rho로 bounded돼 있다는 이야기이다.
즉, 현재 파라미터 $w$에서 그 근방을 살펴볼 것인데, 이 '근방' (neighborhood)의 범위를 제한해주는 역할을 한다.

그리고 $\max_{\epsilon} \mathcal{L}(w + \epsilon) - \mathcal{L}(w)$가 의미하는 것은 결국 현재 파라미터에서의 loss 값에서 가장 크게 loss가 증가하게 만드는 $\epsilon$이 있을때의 값을 의미한다.
그렇다면 결국 loss값이 증가하는데 그 증가하는 속도 (정도)의 차이를 보겠다는 것과 동일하다.
만약 현재 parameter에서 sharp하다면 loss 값이 더 크게 증가할 것이고, flat 하다면 loss 값이 상대적으로 덜 증가할 것이다.
결국 이는 sharpness를 나타내는 항으로 볼 수 있다.
즉, 저자들은 generalization error를 shaprness와 train loss의 합으로 upper bound하였고, 이를 최소화하면 generalization error도 최소화됨을 충분히 기대해볼 수 있는 것이다.
자, 그래서 SAM objective function이 정의가 된다.
$\min_w \max_{\lVert \epsilon \rVert_2 \le \rho} \mathcal{L}(w + \epsilon) + \lambda \lVert w \rVert_2^2$
위 부등식에서 $- \mathcal{L}(w) + \mathcal{L}(w)$는 사라지고 $h()$는 regularization term으로 저자들이 대체하였다.
(사실 h()를 L2-regularization term으로 대체할 수 있는 이유는 논문에서도 자세하게 설명하지 않고 그냥 넘어간다.)
그렇다면 이제 위 objective function을 어떻게 SGD와 같은 알고리즘을 활용해서 최소화할 수 있을까?
우선 이를 위해선 $\epsilon$을 구해야 한다. 하지만 deep neural network의 loss function을 직접적으로 최소화하거나 최대화하는 solution을 구하는 것은 NP-hard 문제이기 때문에 우리가 할 수 있는 것은 approximated solution을 구하는 것이다. 이를 $\hat{\epsilon}$이라 표기하자.
우선 $\mathcal{L}(w + \epsilon) \approx \mathcal{L}(w) + \epsilon^T \nabla \mathcal{L}(w)$이다.
First-order (talyor) approximation을 사용하였다.
우리는 이를 최대화하는 $\epsilon$을 찾는 것이므로, $\max_{\lVert \epsilon \rVert \le \rho} \epsilon^T \nabla \mathcal{L}(w)$를 풀면 된다. 이 문제는 (constrained) linear programming 문제의 형태를 하고 있고 우리는 이 문제를 풀 수 있다.
그래서 도출되는 해는 다음과 같다.
$\hat{\epsilon} = \rho \frac{\nabla \mathcal{L}(w)}{\lVert \nabla \mathcal{L}(w) \rVert}$
이제 $\mathcal{L}(w + \hat{\epsilon})$을 최소화하기 위해 이 함수의 gradient를 계산하면 된다.
$\nabla \mathcal{L}(w)|_{w + \hat{\epsilon}}$
즉 우리는 두 번의 forward , 두 번의 backward를 활용하여서 SAM objective function을 SGD계열의 알고리즘으로 최소화할 수 있다.
우선 $\nabla \mathcal{L}(w)$를 활용해서 $\hat{\epsilon}$을 계산하고 $\nabla \mathcal{L}(w + \epsilon)$을 이용해서 파라미터를 업데이트하는 것이다. 이에 대한 알고리즘은 아래 이미지를 참조하기 바란다.
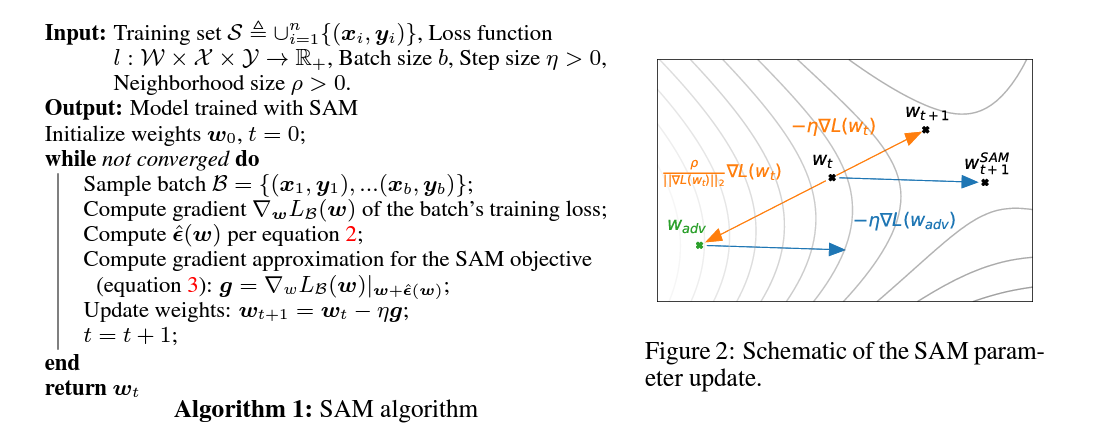
이것이 SAM 알고리즘이다.
SAM은 기존의 SGD 계열의 최적화 알고리즘들과 비교하였을 때 상당히 좋은 성능을 보여주었고, 현재까지도 많은 후속 연구가 이뤄지고 있다.
'Paper Review' 카테고리의 다른 글
| Paper Review: Why Transformers need Adam : A Hessian Perspective (0) | 2025.04.16 |
|---|---|
| Shampoo Optimizer 리뷰 (0) | 2025.03.29 |
| Adam can converge without any modification on Update rules (0) | 2023.07.04 |


댓글