모바일 앱 환경에서는 latex 수식이 깨져 나타나므로 가급적 웹 환경에서 봐주시길 바랍니다.
이번 글에서는 Distributed learning ( Federated learning)으로 유명한 Local SGD 개념에 대해 간략하게 살펴보고자 한다.
이를 살펴보는 이유는 다음에 올릴 글의 주제가 Mini-batch SGD와 Local SGD를 'Random reshuffling' 상황에서 둘의 convergence를 비교하는 내용이기 때문이다.
먼저 간단한 용어들을 살펴보자.
Federated learning의 정의는 다음과 같다.
"Federated learning is a machine learning problem setting where multiple clients collaborate in solving a ML problem, under the coordination of a central server. Each client's raw data is stored locally and not exchanged or transferred; instead, updates intended for immediate aggregation are used to achieve the learning objective."
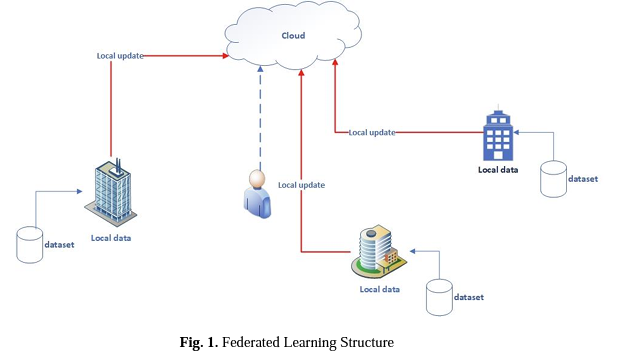
결국 Federated learning (FL) 이란 여러 디바이스 또는 서버 (local server)를 활용하여 '하나의' 모델을 학습하는 ML 방법론을 의미한다. 이때 각 디바이스는 데이터를 가지고 있으며 이 데이터를 활용하여 (local data) 중앙 서버 (Central server)에서는 모델을 학습시키고 이를 다시 local server로 보내는 방식이다.
이때 학습은 중앙 서버에서 이뤄질 수도 있고, local server에서 독립적으로 이뤄진 후, 그 결과만 Central server로 보내져서 합쳐지는 방식으로 이뤄질 수도 있는데 일반적으로 Federated learning은 후자를 의미한다.
즉, local server에서 가지고 있는 local data를 활용해 계산된 gradient를 중앙 서버로 보내서 파라미터 업데이트가 이뤄진 후, local server에 동기화시키거나 또는 local server에서 파라미터 업데이트를 진행한 이후 이 값을 중앙 서버로 보내서 평균을 낸 이후 다시 모든 local server에 동기화시키는 방식등이 존재한다.
이때 '동기화'시키는 것을 FL에서는 'communication' 이라고 한다.
한 번 communiction 하고 다음 번 communication 전까지 그 Term을 'Round'라 하자.
그렇다면 optimization관점에서 Federated learning에는 어떠한 이슈가 있을까?
가장 큰 것은 데이터가 I.I.D 분포를 따른다는 가정이 깨져 버리는 것이다. 각 local server (client)가 독립적으로 gradient를 계산하는데 이 gradient는 local data를 활용해서 계산된 gradient이다.
그리고 이 local data는 다른 client나 central server와 공유되지 않기 때문에 독립적인 분포를 가지고 있고
이는 일반적인 SGD 상황의 I.I.D 분포 가정이 깨지게 한다.
이를 다른 말로는 Heterogeneous data라고 이야기한다.
그렇다면 우리는 어떻게 중앙 서버의 모델을 학습시키는 것일까?
가장 대표적인 알고리즘이 'local SGD'이다.
이를 수식으로 살펴보자.
우리가 학습시키는 모델의 objective function을 $F(x)$라 하고 M개의 local server가 존재한다고 하자.
그렇다면 다음과 같이 표현할 수 있다.
$\min F(x) := \frac{1}{M} \sum_{m=1}^M F_m(x) := \frac{1}{M} \sum_{m=1}^M \mathbb{E}_{z^m \sim D^m} f(x;z^m)$
여기서 $z$는 data를 의미하고 이는 각 local server의 local data이다.
Local SGD는 다음과 같이 학습이 이뤄진다.
$g_{r,k}^m := \nabla f(x_{r, k}^m ; z_{r, k}^m)$
$x_{r, k+1}^m = x_{r, k}^m - \eta_{r, k}^m g_{r, k}^m$
$x_{r+1} = \frac{1}{M} \sum_{m=1}^M x_{r, K}^m$
$m = 1, 2, \cdots, M$이고 $k = 0, 1, \cdots, K-1$이라 하자.
표기가 조금 복잡하게 느껴질 수도 있지만 천천히 살펴보면 전혀 그렇지 않다.
우선 각각의 머신 (m)에서 stochastic gradient를 계산한다.
그리고 각각의 머신 (m)에서 SGD 과정을 진행한다.
이를 각각의 머신 (m)에서 K번 진행한다. (iteration)
그리고 K번 iteration이 진행되면 communication이 진행되며 중앙 서버에서 $x_{r+1}$로 모델의 파라미터를 업데이트하고 다시 이를 각 local server에 동기화시킨다.
이것이 가장 기본적인 Local SGD의 알고리즘이다.
자 이는 parameter를 평균을 내는 방식의 알고리즘이다.
하지만 앞서 이야기한 것처럼 gradient를 평균내서 중앙 서버에서 파라미터를 업데이트한 이후, 다시 이를 local server에 동기화시키는 Mini-batch SGD의 FL버전도 있다.
이 둘을 비교한 논문은 여럿 있으며 추후 기회가 된다면 소개하겠다.
자, 그러면 다음 글에서 Local SGD와 Mini-batch SGD의 FL 버전을 Random Reshuffling (RR) 이 적용된 상황에서 convergence analysis를 수행한 논문을 살펴보자.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into Optimization : Types of Convergence (0) | 2023.11.05 |
|---|---|
| Optimization 심화 : well-known inequality (0) | 2023.09.25 |
| Optimization 심화 : Random Reshuffling (2) (1) | 2023.09.04 |
| Optimization 심화 : Random Reshuffling (1) (0) | 2023.08.31 |
| Optimization 심화 : SGD (3) (0) | 2023.08.26 |

댓글