"모바일 앱 환경에서는 latex 수식이 깨져서 나타나므로, 가급적 웹 환경에서 글을 읽어주시기 바랍니다. :)"
"What is the cross-entropy loss?" (part 2.)
오늘은 크로스-엔트로피 손실 함수에 대한 두 번째 설명이다.
(첫 번째 설명은 위 글을 참조하기 바랍니다. https://kyteris0624.tistory.com/13)
Deep dive into optimization part 2. 손실함수와 최적화
****모바일 앱 환경에서는 latex 수식이 깨져서 나타나므로, 가급적 웹으로 보시길 추천드립니다. *** "Which loss functions are used in deep learning optimization?" 오늘은 딥러닝 최적화 상황에서 자주 쓰이는
kyteris0624.tistory.com

$p(x)$는 true distribution (e.g., label distribution) 이고, $q(x)$는 model output distribution이다.
$\sum$ 대신 Expectation ($\mathbb{E}$) 이 들어가도 된다.
지난 포스팅에서는 크로스 엔트로피를 최소화하는 것이 (binomail or multinomial) log likelihood를 최대화하는 것이라고 이야기하였다.
오늘은 정보이론의 관점에서 크로스 엔트로피 손실 함수 (cross-entropy loss function)를 설명하고자 한다.
우선 '정보' (information)가 무엇인지 살펴보자.
정보는 특정한 관찰에 의해 얼마만큼의 정보를 획득했는지 수치로 정량화한 값이다.
즉, 정보량은 자주 발생하는 관찰 / 사건 (또는 확률이 큰 사건)에 대해서는 작은 값을 갖지만, 자주 발생하지 않는 사건 (확률이 작은 사건)에 대해서는 큰 값을 갖는다.
특정한 관찰이나 사건 A의 정보량 $I(A)$은 다음과 같이 정의된다.

A가 발생할 확률이 클수록 정보량 $I(A)$은 작아짐을 알 수 있다.
엔트로피 (entropy)는 정보량의 평균 (평균 정보량)이다.
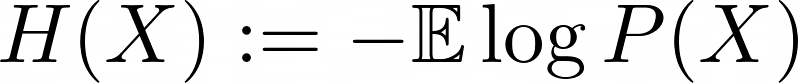
만약 확률변수 $X$가 이산확률변수이면, 기댓값은 $\sum$으로 연산될 것이고, 연속확률변수이면 $\int$으로 연산될 것이다.
만약에 이산확률변수 $X$가 균일분포 (uniform distribution)를 따른다면, 엔트로피가 최대일 것이다.
직관적으로 이는 당연한데, 균일분포를 따른다는 것은 사건의 각 결과들이 나타날 확률이 모두 동일하다는 것이고, 이때 우리는 특정한 결과가 나타났을 때 평균적으로 가장 큰 정보를 얻을 것이다.
실제 위 정의로 계산해도 확인 가능하다.
쿨백-라이블러 발산 (KL-divergence)은 두 확률분포의 차이를 측정하는 지표이다.
편의상 확률분포의 '거리' (distance)라고 표현하는 곳도 있는데, KL-divergence는 거리의 공리적 조건 중 '대칭성'을 만족하지 않기 때문에, 거리라고 정의할 수는 없다.
** Metric (or distance)의 3가지 공리.
두 대상 $x$, $y$ 사이의 거리 함수는 다음과 같은 조건을 만족하는 함수 $d(x, y)$로 정의된다.
여기서 두 대상이라 함은 집합도 가능하고 집합의 원소도 가능하다.
1. $d(x, y) \ge 0$ -> Non-negative
2. $d(x, y) = d(y, x)$ -> 대칭성
3. $d(x, y) = d(x, z) + d(z, y)$ -> 삼각부등식
KL-divergence는 2번의 조건을 만족하지 않기 때문에 거리라 정의할 수 없다. 이는 KL의 정의를 활용하면 확인이 가능하다.
확률변수 X에 대해서 두 확률 P, Q에 의한 확률분포가 주어져있다고 하자. 서로 다른 확률을 갖기 때문에 확률분포도 다를 것이다.
그리고 각각의 확률분포 함수를 $f_P$, $f_Q$라고 하자.
이때 두 분포의 다름 정도를 정량적으로 측정하기 위해, KL-divergence를 사용하는데 정의는 다음과 같다.

KL-divergence는 두 분포간의 차이를 나타내기 때문에 동일한 분포에 대해서는 값이 0이다.
그리고 $(f_P||f_Q)$와 $(f_Q||f_P)$가 다르다는 것은 정의를 통해 자명하기 때문에 대칭성이 성립하지 않고, 거리로 볼수는 없다.
만약 여기서 $Q$가 참 분포 (true distribution)을 나타내고, $P$가 모델 아웃풋의 분포를 나타내며, P가 Q에 가까워지게, 즉 KL-divergence가 작아지게 한다면 우리는 좋은 분류 (classification) 모델을 갖게 될 것이다.
이를 우리는 크로스 엔트로피 손실함수를 최소화하면서 수행할 수 있는데, cross entropy를 최소화하는 것이 결국 KL-divergence를 최소화하는 것과 동일하기 때문이다.
$D_K(f_P||f_Q) = P(X) \log P(X) - P(X) \log Q(x)$
여기서, $P(X) \log P(X)$는 True distribution이므로 모델의 parameter에 따라서 값이 변화하지는 않는다.
모델 파라미터에 의해 영향을 받는 term은 model output distribution ($Q(X)$)이고 $-P(X) \log Q(x)$는 크로스엔트로피의 정의이므로 이를 최소화하는 것이 결국 KL-divergence를 최소화하는 것과 동일하다.
즉, 말로 표현하면 KL-divergence는 cross-entropy -entropy인데 entropy는 최적화의 대상이 되지는 않으므로, cross entropy를 최소화하는 것은 KL-divergence를 최소화하는 것과 동일하다는 의미이다.
이로서 cross-entropy loss의 의미에 대한 설명을 마치도록 하겠다.
다음 포스팅에서는 convex, smooth, strong-convex에 대해서 다루도록 하겠다.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into optimization : Gradient descent - Updated (0) | 2023.03.20 |
|---|---|
| Deep dive into optimization: Gradient descent - Updated (0) | 2023.03.16 |
| Deep dive into optimization: Convexity - Updated (0) | 2023.03.11 |
| Deep dive into optimization part 2. 손실함수와 최적화 (Updated) (2) | 2023.03.06 |
| Deep dive into Optimization Part 1. 최적화란 무엇인가? (Updated) (2) | 2023.03.04 |




댓글