"모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 pc 웹 환경에서 읽어주시기 바랍니다."
"What is the convex?"
오늘은 최적화 개념 중 매우 중요하면서 가장 기본이 되는 개념인 convexity에 대해 살펴보도록 하겠다.
수학적 최적화 연구에서는 알고리즘의 수렴성 분석 (convergence analysis), 수렴 속도 분석 (convergence rate) 등이 매우 중요한 주제이고, 추후 Deep dive into optimization 시리즈에서도 여러 번에 걸쳐 살펴볼 예정인데 그때 손실함수 (Loss function)에 대해 여러 가지의 가정들을 하고 분석이 이뤄진다.
그때 가장 많이 등장하는 가정이 1. Convex 2. Smoothness 3. Strong-convex가 있는데 오늘은 이 3가지에 대해 기본적인 정의와 개념 몇 가지 성질들을 살펴보고자 한다.
1. Convex (볼록성)
우선 함수의 볼록성을 정의하기 이전에 볼록한 집합 (Convex set)에 대해 먼저 정의해야 한다.
Convex set의 정의는 다음과 같다.

위 두 개의 그림 중 위 이미지는 convex set이고, 아래 이미지는 non-convex set이다.

어떤 집합 $C$가 있을 때 그 집합의 임의의 두 원소 $x_1, x_2$의 'convex sum', 즉 0과 1 사이의 임의의 스칼라 $\alpha$에 대해,
$\alpha x_1 + (1 - \alpha) x_2$도 항상 집합 $C$의 원소이면, 그 집합을 convex set이라고 표현한다.
위 그림을 통해 직관적으로 이해해보면, $\alpha x_1 + (1 - \alpha) x_2$ 는 $x_1, x_2$를 연결한 선분이다.
이 선분이 집합에 온전히 포함될 때 그 집합을 convex set이라고 부르므로, 그 집합은 결국 아래 그림과 같이 움푹 파인 부분이나, 역으로 튀어나온 부분이 없어야 한다.
convex function으로 넘어가기 전에 한 가지 유용한 공식을 이야기하고 넘어가겠다.
함수 $f : U \rightarrow \mathbb{R}$이 open set $U \subseteq \mathbb{R}^n$ 두 번 미분 가능하고, $r > 0$에 대해, $B(x, r) \subseteq U$를 만족한다고 하자. 그러면 $y \in B(x, r)$에 대하여, 다음을 만족하는 $\xi \in [x, y]$가 존재한다.
$f(y) = f(x) + \langle \nabla f(x), y - x \rangle + \frac{1}{2} (y - x)^T \nabla^2 f(\xi) (y - x)$
이를 'linear approximation theorem'이라고 부른다.
그렇다면 convex function은 무엇일까?

역시나 여기서도 $x_1, x_2$는 함수 정의역의 원소이고, $\alpha$는 $0 \le \alpha \le 1$을 만족하는 임의의 실수이다.
그리고 중요한 전제조건은 함수 $f$의 정의역이 'convex set'이어야 한다는 것이다.
그림으로 보면 이해가 잘 될 것이다.
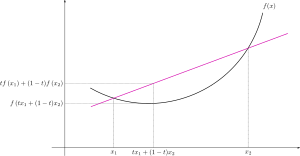
함수의 임의의 두 점을 잡고 그것을 연결한 선분 ($(1 - \alpha) f(x_1) + \alpha f(x_2)$)보다 함수가 아래에 있을 때 그 함수는 convex function이다.
하지만 convex function의 정의는 이것 하나가 아니다.
함수가 적어도 1번 미분 가능할때, 적어도 2번 미분 가능할 때 convex function의 정의가 있는데 이는 다음과 같다.
'적어도 1번 미분 가능한 볼록 함수 정의'

여기서 $\nabla f(y)$는 $f(x)$의 $y$에서의 접선의 기울기이다. (gradient)
이 정의가 의미하는 것은 다음과 같다.
convex function은 임의의 점에서의 접선보다 그래프가 항상 위에 있다.
$f(y) + \nabla f(y)^T (x - y)$는 $y$에서의 접선을 의미하고 임의의 $x$에 대해서 항상 f(x)가 접선에서의 $x$값보다 크므로, 곡선이 접선 위에 있다는 의미로 해석될 수 있다.
'적어도 2번 미분 가능한 볼록 함수 정의'

$\preccurlyeq$은 $f(x)$가 일변수함수 ($f : \mathbb{R} \rightarrow \mathbb{R}$) 일수도 있지만, 다변수함수 ($f : \mathbb{R}^n \rightarrow \mathbb{R}^m$) 일수도 있고 이 경우에는 두 번 미분하면 '행렬'이 나오기 때문에 (이를 우리는 Hessian matrix라 한다.) 행렬과 수의 대소비교는 $\preccurlyeq$으로 표기하는 것이 일반적이다.
위 부등식의 의미는 Hessian matrix가 양의 준정부호 행렬 (Positive semi-definite) 이란 의미이고, $f(x)$가 일변수 함수일 때는 항상 0보다 크다는 뜻이다.
$f(x)$가 일변수함수인 경우로 직관적 설명을 해보자면, 이계도함수는 도함수의 도함수이므로 이계도함수가 0보다 크다는 것은 도함수가 증가한다는 의미이고 점점 커진다는 의미이다. 이렇게 되도록 함수를 그려보면 자연스레 볼록한 모양의 함수가 나올 수밖에 없다.
자 여기까지 convex function의 정의들을 살펴보았고 convex function은 어떠한 성질이 있는지 살펴보자.
최적화에서 볼록 함수가 갖는 아주 중요한 성질이 있는데 'local minimum이 global minimum이라는 것'이다.
그리고 만약 볼록함수가 적어도 한 번 미분 가능한 함수라면 local minimum (= global minimum)은 아주 중요한 성질이 하나 있는데 그 지점에서 기울기가 0이라는 것이다.

즉, 모든 local minimum(이자 global minimum) $x^*$에 대해서 항상 기울기가 0이다.
그리고 두 번째로 특히 딥러닝/머신러닝 최적화에서 볼록 함수가 또 중요한 이유는 실제로 많은 머신 러닝의 최적화 문제가 볼록 함수의 최적화 문제로 표현이 가능하다는 것이다. (re)formulation
이것을 여기서 하나하나 다 살펴보진 않겠지만, SVM, ridge regression, logistic regression, LASSO 등 많은 머신 러닝 문제들이 볼록함수의 최적화 문제로 표현이 된다. 이를 우리는 'convex optimization problem'이라고 한다.
이러한 이유들로 convex function에 대해서는 정확하게 이해하고 그것들이 어떤 성질을 갖고 있는지는 공부해둘 필요가 있다.
다음은 Smoothness이다.
이 또한 딥러닝 / 머신러닝 최적화 문제에서 자주 등장하는 가정이자 중요한 성질로 이번 포스트에서 그 정의를 살펴보고자 한다. 여기서의 smooth는 해석학에서의 smooth와는 정의가 다르다.
어떤 함수 $f(x)$가 L-smooth하다는 것은 함수 $f(x)$의 gradient가 Lipschitz constant $L$에 대해서 Lipschitz continuous함을 의미한다.
*립시츠 연속 (Lipschitz continuous) 함수 (function)
어떤 함수가 상수 L에 대해 립시츠 연속임의 정의는 다음과 같다.

직관적으로 이는 함수의 변화 폭을 제한하는 것과 같은데 $L$이 작을 수록 함수의 변화 폭이 크지 않다는 것을 의미한다.
즉, 이는 바꿔말하면 $x$와 $y$사이의 거리가 크지 않을수록 $f$의 $x$에서의 함숫값과 $y$에서의 함숫값 차이도 크지 않다는 것이다.
이는 함수가 급격하게 증가하거나 급격하게 감소하는 것을 제한하는 것으로 받아들일 수 있다.
그렇다면 $\nabla f(x)$가 립시츠 연속이라는 것은 다음과 같이 표현할 수 있다.

이것이 함수 $f(x)$의 L-smooth의 정의이다.
최적화 논문에서 매우 자주 쓰이는 가정이고 중요한 성질이기 때문에 자세하게 알아보자.
먼저 $L$에 대한 이야기이다. $L$은 Lipshcitz constant (립쉬츠 상수)라 부르고, 함수에 대해 이 값을 Tight하게 예측하는 것도 매우 중요하다.
예를 들어 $f(x) = x^2$을 생각해보자. $f^{\prime}(x) = 2x$이고 위 수식에 대입해보면 $L \ge 2$는 위 식을 만족한다.
우리는 $L$ 값중 가장 작은 값을 찾는 것이 중요하므로, $L = 2$로 두는 것이 좋다.
즉, $L$-smoothness 정의에 의하여, $L_1$-smooth한 함수는 $L_2 \ge L_1$인 $L_2$에 대하여, $L_2$-smooth도 만족한다. 하지만, 더 Tight한 값은 $L_1$이므로 립쉬츠 상수를 $L_1$으로 두는 것이 좋다.
그 이유는 Gradient descent 부분에서 설명하겠다.
다음은 $L$-smooth 함수가 갖는 성질에 대한 이야기이다.
가장 첫 번째로 이야기할 것은 Descent Lemma이다. 이는 다음과 같다.
$f(y) \le f(x) + \langle \nabla f(x), y - x \rangle + \frac{L}{2} \lVert y - x \rVert^2$.
이에 대해선 증명과정을 보도록 하겠다.
Fundamental theorem of calculus에 의하여,
$f(y) - f(x) = \int_{0}^{1} \langle \nabla f(x + t(y - x)), y - x \rangle dt$. 이므로,
$f(y) - f(x) = \langle \nabla f(x), y - x \rangle + \int_{0}^{1} \langle \nabla f(x + t (y - x)) - \nabla f(x), y - x \rangle dt$ 이고
따라서
$|f(y) - f(x) - \langle \nabla f(x), y - x \rangle | = |\int_{0}^{1} \nabla f(x + t (y - x)) - \nabla f(x), y - x \rangle dt |$
$\le \int_{0}^{1} |\langle \nabla f(x + t (y - x)) - \nabla f(x) , y - x \rangle | dt$
$\le \int_{0}^{1} \lVert \nabla f(x + t( y- x)) - \nabla f(x) \rVert \cdot \lVert y - x \rVert dt $
$\le \int_{0}^{1} t L \lVert y - x \rVert^2 dt$
$= \frac{L}{2} \lVert y - x \rVert^2$.
세 번째 식 (부등식)에서는 코시-슈바르츠 부등식을 사용하였다.
다음은 두 번 미분 가능한 함수 $f(x)$에 대하여 $L$-smoothness의 equivalene condition이다.
$\Vert \nabla^2 f(x) \rVert_2 \le L$,
즉, Hessian 의 $L_2$-norm이 $L$보다 작다.
추가적으로 만약 함수가 convex하다면, Hessian matrix의 최대 고윳값 (maximum eigenvalue)가 $L$보다 작다는 것도 보일 수 있다.

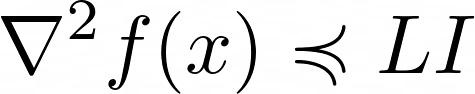
두 번째 부등식은 f라는 함수가 완만하게 변화한다, 즉 우측의 이차함수보다 위에 있지 않다(=크지 않다)라는 것을 의미한다. 그리고 이는 Descent Lemma라 하여, 수렴성 분석에서 매우 자주 쓰이는 가정 및 공식이다.
맨 아래 부등식은 $f(x)$의 Hessian matrix가 Identity matrix를 L배 한 것 보다 작다는 것이고 이는 고윳값이 L보다 작다와 동치이다.
고윳값은 다변수함수에서 특정한 방향(고유벡터 방향)으로의 변화율을 나타내는데, 이것이 $L$보다 작다는 것은 그 방향으로의 변화율 크기를 제한 (Upper bound)하는 것과 같은 의미이다.
이처럼 smoothness는 어떤 함수의 변화 정도를 제한하는 성질이다.
하나만 더 첨언을 하면 smooth는 함수의 볼록성과는 독립적인 성질이다. 즉, 함수가 볼록하든 볼록하지 않든 smoothness는 가질 수 있다.
마지막으로 strong-convex에 대해 이야기하고 마치자.
strong convex의 중요한 성질은 'local minimum이 global minimum이고, 유일한 local minimum을 가진다'이다.
함수 $f : E \rightarrow (-\infty, +\infty]$가 어떤 $\sigma > 0$에 대하여, 정의역 $E$가 convex하고, $\lambda \in [0, 1]$에 대하여 다음을 만족하면 $\sigma$-strongly convex하다고 정의한다.
$f(\lambda x + (1 - \lambda) y) \le \lambda f(x) + (1 - \lambda) f(y) - \frac{\sigma}{2} \lambda (1 - \lambda) \lVert x - y \rVert^2$
함수가 한 번 미분이 가능하면 다음과 같은 equivalence condition이 있다.
$f(y) \ge f(x) + \langle \nabla f(x), y - x \rangle + \frac{\sigma}{2} \lVert y- x \rVert^2$
$\langle \nabla f(y) - \nabla f(x), y - x \rangle \ge \sigma \lVert y - x \rVert^2$.
Strongly convex의 중요한 성질은 다음과 같다.
"$f(x)$가 convex 하다" = $f(x) + \frac{\sigma}{2} \lVert \cdot \rVert^2$가 strongly convex하다.
즉, 두 조건은 if and only if 관계이고, 이는 손실함수 $f$가 convex하다면, 거기에 우리가 어떤 norm을 regularization term으로 더한 loss function은 strongly convex하다는 것을 알려준다.
이제 다음 블로그에서부터 gradient descent를 이야기하는 것으로 본격적인 최적화가 시작된다.
앞으로 다룰 다양한 (그리고 자주 쓰이는) 딥러닝 optimization algorithm들을 이야기할 때, 위에 함수 성질들을 가정하는 경우가 종종 있을 터인데 그런 의미에서 오늘 포스팅은 매우 중요한 내용이라 할 수 있다.
위에서 언급한 내용 말고도 볼록함수, L-smooth 함수의 성질들이 더 많이 있는데 이는 앞으로 기회가 될 때 필요한 곳에서 언급해나가도록 하겠다.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into optimization : Gradient descent - Updated (0) | 2023.03.20 |
|---|---|
| Deep dive into optimization: Gradient descent - Updated (0) | 2023.03.16 |
| Deep dive into optimization part 3 - Updated (0) | 2023.03.08 |
| Deep dive into optimization part 2. 손실함수와 최적화 (Updated) (2) | 2023.03.06 |
| Deep dive into Optimization Part 1. 최적화란 무엇인가? (Updated) (2) | 2023.03.04 |






댓글