*** 모바일 앱 환경에서는 latex 수식이 깨져서 나타나므로, 가급적 웹 환경에서 읽어주시길 바랍니다 :) ***
"Linear algebra, Probability and Statistics, Calculus review"
오늘은 지난 번에 이어서 확률통계 2번째 글로 유명한 확률분포, 다중확률변수에 대해 이야기해보고자 한다.
다음 글에서는 통계적 추정에 대한 간단한 맛보기, 미적분에 대한 복습을 마지막으로 딥러닝을 위한 기초수학은 마무리하겠다.
1. Binomial distribution (이항 분포)
이항 분포를 이야기하기 위해서는 먼저 베르누이 시행 (Bernoulli experiment)을 이야기해야 한다.베르누이 시행이란 시행의 결과가 두 가지 중 하나로만 나오는 시행을 의미한다. 베르누이 시행도 random experiment이므로 시행 결과로 나올 수 있는 두 가지는 mutually exclusive, exhaustive하다.대표적으로 양성 / 음성, 남자 / 여자, 참 / 거짓 등등이 존재하는데 이 때 하나의 결과가 나올 확률이 $p$라면, 다른 하나의 결과가 나올 확률은 $1 - p$라고 이야기 할 수 있다.
Random variable $X$가 베르누이 시행의 확률변수라고 하자.
그렇다면 $X(\text{success}) = 1, X(\text{failure}) = 0이라 하고, P(X = 1) = p, P(X = 0) = 1-p$라 할 수 있다.
확률 변수의 값은 셀 수 있으므로 베르누이 시행을 따르는 확률 변수는 '이산 확률 변수'이고 그것의 확률분포는 확률질량함수 (PMF)로 나타낼 수 있다.
$p(x) = p^x (1-p)^{1-x}, \quad x \in \{0, 1\} $.
이항 분포란, 총 $n$번의 베르누이 시행을 하였을 때 특정한 사건이 $x$번 관측될 확률분포를 의미한다.
이 때 각 시행은 서로 "독립"이며, 사건이 발생할 확률이 $p$로 고정되어져 있어야 한다.
그렇다면 어떤 확률변수 $X$가 이항 분포를 따른다면 확률 변수의 값도 셀 수 있으므로 이 확률변수는 '이산 확률 변수'이고 그것의 확률분포도 역시나 PMF로 나타낼 수 있다.
먼저 총 $n$번의 시행에서 $x$번 성공이 발생할 경우의 수는 $_{n}C_{x}$이고 확률은 $p^x (1-p)^{n-x}$이므로,
확률 질량 함수는 다음과 같다.
$p(x) = _{n}C_{x} p^x (1-p)^{n-x}, \quad x \in \{ 0, 1, 2, \cdots, n \}$
위와 같은 확률 질량 함수를 가지는 확률변수 X를 우리는 "이항분포를 따른다"라고 표현한다.
이항 분포의 평균과 분산은 각각 다음과 같다. $\mathbb{E}(X) = np, V(X) = np(1-p)$.
2. Poisson distribution (포아송 분포)
어떤 확률 변수 X의 확률 분포 함수가 양수 $\lambda$에 대해서 다음과 같이 정의된다고 하자.
$p(x) = \frac{\lamda^x e^{-\lamda}}{x!} \quad, x = 0, 1, 2, \cdots$
이러한 확률 분포 함수를 갖는 확률 변수 X를 우리는 포아송 분포를 따른다고 이야기하고 모수 $\lambda$를 갖는 포아송 분포를 따른다고 이야기한다.
포아송 분포의 평균과 분산은 모두 $\lambda$이다.
이산확률변수에는 위의 분포들을 제외하고도 기하 분포, 음이항 분포 등등 더 많이 있지만 이러한 것은 딥러닝 기초에서 자주 접하지는 않기 때문에 넘어가도록 하겠다.
다음은 연속 확률 변수의 분포들이다.
3. $\Gamma$- distribution (감마 분포)
감마 분포에 대해서 이야기하기 위해서는 먼저 감마 함수에 대해 정의하여야 한다.
감마 함수는 다음과 같이 정의된다.
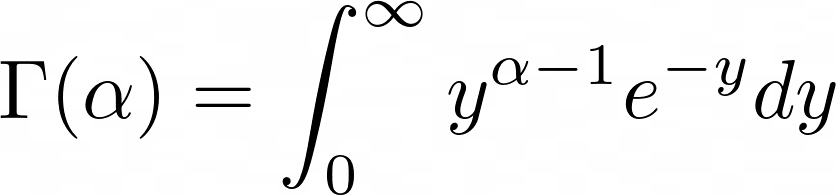
만약 $\alpha=1$이면, 감마함수 값은 1이다. 즉, $\Gamma(1) = 1$이다.
만약 $\alpha > 1$인 정수이면, 감마함수는 factorial꼴로 표현할 수 있다.
즉, 다음과 같은 성질을 가지고 있다.
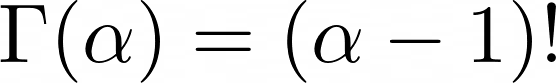
어떤 확률 변수 $X$가 $\Gamma$-distribution을 따른다면 다음과 같은 확률 밀도 함수 (PDF)를 갖는다.

확률 변수 $X$가 가질 수 있는 값은 $0 < x < \infty$이다.
또한, 감마 분포는 pdf에서 볼 수 있듯이 모수 (parameter) $\alpha$, $\beta$를 가지는데 이 둘은 모두 0보다 커야 한다.
감마 분포의 평균은 $\alpha \beta$이고, 분산은 $\alpha \beta^2$이다.
4. $\Xi^2$-distribution (카이제곱 분포)
$\Xi^2$-distrbution은 감마 분포의 특수한 형태로 $\alpha = \frac{r}{2}$이고, $\beta = 2$일 때 확률변수 $X$가 모수 $r$을 갖는 카이제곱 분포를 따른다고 이야기한다.
PDF도 감마 분포의 PDF에 $\alpha, \beta$를 대입하면 유도가 된다.
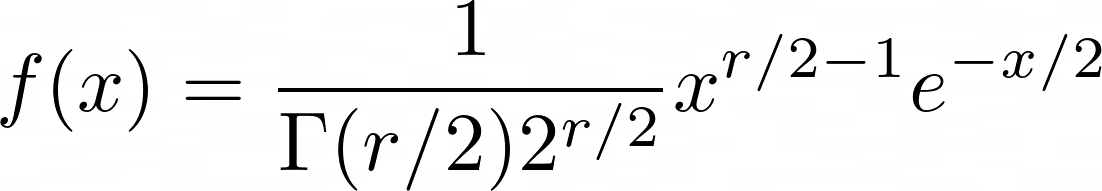
카이제곱 분포의 평균은 $r$이고, 분산은 $2r$이다.
5. $\beta$-distribution (베타 분포)
베타 분포를 이야기하기 위해서는 먼저 다중 확률 변수 (Multivariate random variable)을 이야기해야 한다.
* Random vector
Sample space $\mathcal{C}$에서의 random experiment를 수행할 때, 두 확률 변수 $X_1$, $X_2$가 있다고 해보자.
각각의 확률변수가 $c \in C$에 대해 실수값으로 사상시킨다고 할 때, 즉 $X_1(c) = x_1, X_2(c) = x_2$, 우리는 이 순서쌍 $(X_1, X_2)$를 random vector라 한다. 그리고 $(X_1, X_2)$의 공간은 순서쌍 $D = {(x_1, x_2) : x_1 = X_1(c), x_2 = X_2(c), c \in C}$의 집합이다.
만약 random vector $(X_1, X_2)$의 공간 $D$가 셀 수 있다면 (finite), 이산 확률 변수이고, 그 때 결합 확률 질량 함수 (Joint probability mass function)는 다음과 같이 정의된다.
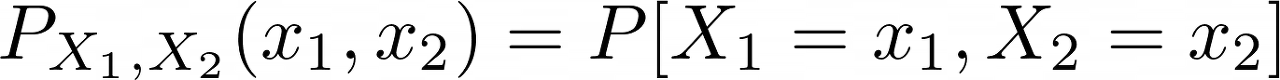
또한 만약 random vector $(X_1, X_2)$의 공간 $D$가 연속적이라면 (=즉 누적 확률 분포 함수, CDF가 연속적이라면)
CDF $F_{X_1, X_2}(x_1, x_2)$는 다음과 같이 표현될 것이고,
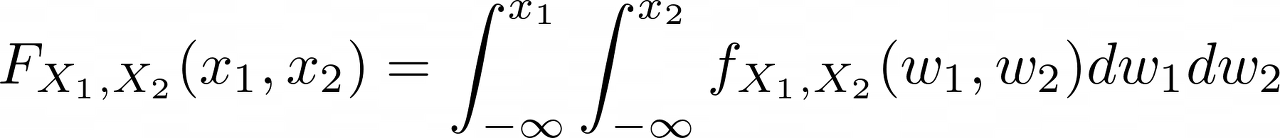
이를 미분해서 나오는 joint probability density function $f_{X_1, X_2}(x_1, x_2)$은 다음과 같이 정의된다.
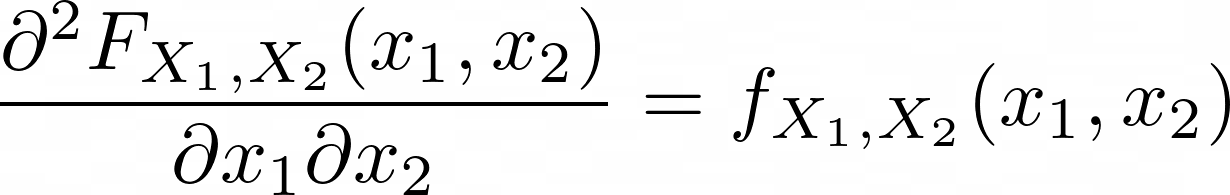
지금 우리는 random vector의 원소가 2개의 확률 변수인 경우를 예시로 들어 살펴보았지만 이것이 임의의 n개로 확장되면 그것이 곧 다중 확률 변수의 분포, Multivariate distribution이 된다.
자 그렇다면 베타 분포란 무엇일까?
$\beta$-distribution은 독립인 두 확률 변수 $X_1, X_2$가 $\Gamma$-distribution을 따르는 확률변수라 할 때, 다음과 같은 새로운 확률 변수를 정의해보자.
$Y_1 = X_1 + X_2$
$Y_2 = \frac{X_1}{X_1 + X_2}$
이 때 우리는 이 두 확률 변수의 결합 확률 밀도 함수, Joint PDF를 정의할 수 있고, 이를 통해서 $Y_2$의 marginal pdf 도 유도할 수 있다. 복잡한 계산과정은 스킵하자.

$0 < y_2 < 1$에 대해 위와 같은 PDF를 갖는 확률 변수를 우리는 베타 분포를 따른다고 이야기한다.
6. 정규 분포 (Normal distribution)
다른 말로 가우시안 분포라고도 하는 정규 분포는 여러 확률 분포들 중에서 가장 중요한 분포이다.
먼저 정규 분포의 모습을 보자.

왼쪽은 단일 분포 (확률변수 하나)로서의 가우시안 분포이고, 오른쪽은 다중 분포 (성분이 두 개인 확률벡터)로서의 가우시안 분포의 모습이다. 각각의 pdf는 다음과 같다.

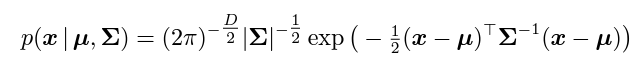
이 때 $\mu$가 평균이고 $\sigma^2$가 분산이다.
아래의 pdf는 Multivariate gaussian distribution의 pdf로서 $\mu$는 mean vector이고 $\Sum$은 covariance matrix이다.
covariance matrix, 즉 공분산 행렬이란 각각의 성분이 확률변수들 사이의 분산인 행렬로서 위 예시에서는 확률 변수가 2개이므로 공분산 행렬은 2행 2열 행렬이 되고, 각각의 성분은 확률 변수 $Var(X_1, X_1), Cov(X_1, X_2), Cov(X_2, X_1), Var(X_2, X_2)$가 된다. 여기서 알 수 있듯이 공분산 행렬의 주대각 성분은 분산이 되고, 대칭 행렬이다.
확률 변수 $X$가 평균이 $\mu$이고 분산이 $\sigma^2$인 정규분포를 따른다는 것은 다음과 같이 표현한다.
$X \sim \mathcal{N}(\mu, \sigma^2)$.
다음 글은 딥러닝을 위한 기초수학 마지막 챕터로서, 통계적 추정과 미적분에 대한 이야기로 마무리하고자 한다.
'Deep dive into Deep learning' 카테고리의 다른 글
| Deep dive into Deep learning part 9 - Updated (0) | 2023.04.02 |
|---|---|
| Deep dive into Deep learning part 8. - Updated (0) | 2023.03.29 |
| Deep dive into Deep learning part 6. - Updated (0) | 2023.03.17 |
| Deep dive into Deep learning part 5. - Updated (1) | 2023.03.13 |
| Deep dive into Deep Learning Part 4. - Updated (0) | 2023.03.09 |




댓글