*** 모바일 앱 환경에서는 latex 수식이 깨져서 나타나므로, 가급적 웹 환경에서 읽어주시길 바랍니다 :) ***
"Linear algebra, Probability and Statistics, Calculus review"
오늘은 선형대수학 마지막 복습의 글이다.

선형대수학에서 매우 중요한 방정식 중 하나이다.
먼저 스칼라 / 벡터 / 행렬을 구분하자면,
$A \in \mathbb{R}^{n \times n}$, $x \in \mathbb{R}^{n}$, $\lambda \in \mathbb{R}$이다.
이때 정의상, 고유벡터는 '영벡터가 아닌' 벡터이기 때문에, 위 방정식의 해에서 $x = 0$은 자동적으로 제외된다.
영벡터가 아닌 위 방정식을 만족하는 해, $x$를 고유벡터 (eigenvector), 그때의 실숫값 $\lambda$를 고윳값 (eigenvalue)라 한다.
먼저 간단하게 위 방정식을 푸는 방법, 그리고 고유벡터와 고윳값과 관련된 성질들을 살펴보자.
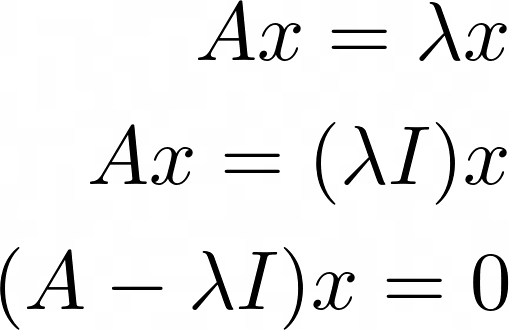
이 때 $x$는 영벡터가 아니므로, 위 방정식에 해가 존재하기 위해서는 (즉, 해가 없는 상황을 제외하려면)
$A - \lambda I$가 역행렬이 없어야 한다.
왜 역행렬이 없어야 할까?
만약 위 행렬이 역행렬이 존재한다면, 양변에 $(A - \lambda I)^{-1}$를 곱하면 $x = 0$이 되기 때문에 고유벡터 정의에 위배된다. 즉, 위 방정식을 만족하는 해가 $x = 0$으로 유일한 해만 존재하기 때문에 이러한 상황은 배제하는 것이다.
그래서 역행렬이 존재하지 않는 경우만 고려한다.
그렇다면, 역행렬이 없는 상황에서 $x$ 해가 존재하기 위해서는 결국 '해가 무수히 많다'라는 상황만 성립된다.
해가 없는 경우면 결국 고유벡터도 없는 것이기 때문에 그것을 논의할 필요는 없다.
여기서 우리는 만약 어떤 행렬의 고유벡터가 존재한다면 그것은 무수히 많을 수밖에 없다는 것을 알 수 있다.
일반적으로 역행렬이 없는 경우 우리는 '판별식 = 0' 방정식을 세우고 풀기 때문에 이 문제도 그렇게 풀어나가면 된다.

그러면 고윳값과 고유벡터를 구하는 법은 알겠는데, 이게 무슨 의미가 있는 것일까?
우리는 어떤 x라는 벡터에 행렬 A를 곱하는 것 $Ax$를 벡터 $x$의 선형변환으로 볼 수 있다.
이전 글에서 행렬과 벡터의 곱셈은 행렬의 열벡터의 '선형결합'이라고 볼 수 있다고 하였다.
즉, 행렬의 열벡터를 기저 (basis)로 갖는 어떤 벡터 공간 (=column space)에 $Ax$라는 벡터가 원소로 존재하는 것을
의미하고, 이는 기존 벡터공간의 기저 (basis)가 새로운 벡터공간기저로 변환된 것으로 볼 수 있다.
즉, 하나의 벡터 공간에서 다른 벡터 공간으로의 사상 / 변환을 우리는 행렬과 벡터의 곱셈으로 볼 수 있다.
정확히 말하면 행렬을 곱하는 것은 '선형 변환'이라고 하는데 선형성을 만족하기 때문이다.
(선형성 정의는 이전 포스팅 글 참조)
그렇다면 어떤 벡터를 원래의 벡터 공간에서 다른 벡터 공간으로 변환시키는데, 이때 그 벡터가 놀랍게도 방향이 바뀌지 않고 오직 크기만 증가 / 감소하는 벡터들을 고유벡터라고 한다. 그리고 '몇 배' 증가하는가? 감소하는가? 등을 나타내는 수치가 고윳값이다.
즉, 고유벡터는 행렬 A에 의해 선형 변환이 되더라도 방향이 바뀌지 않고 크기만 변화하는 벡터를 고유벡터라 한다.
그리고 행렬 $A$를 고유벡터와 고윳값들을 활용해 표현이 가능한데 이를 우리는 Eigendecomposition ( =Diagonalization)이라 한다.
이에 대해 알아보자.

$A \in R^{n \times n}, P \in R^{n times n}, D \in R^{n \times n}$.
위 등식에서 $D$는 대각 행렬 (Diagonal matrix)라고 부른다.
대각 행렬은 주 대각성분을 제외한 나머지 성분이 모두 0인 행렬을 의미하는데 $D$에서의 주 대각성분은 모두 고윳값이다.
그리고 $P$는 열벡터가 고유 벡터인 행렬이다.
자, 그렇다면 대각화가 언제 가능한지 위 정의를 통해 알 수 있다. 그렇다.
$P^{-1}$이 존재할 때 우리는 어떤 행렬 A를 대각화할 수 있다.
그렇다면 언제 역행렬이 존재할까?
앞서 포스팅에서 이야기했듯 모든 열벡터가 선형독립이어야 역행렬이 존재한다.
이는 곧 $P$에서는 열벡터가 $A$의 고유벡터들이므로, $A$의 n개의 고유벡터들이 모두 선형독립이어야 우리는 $A$ 행렬이 대각화가 가능하다고 이야기할 수 있다. 이 말은 $A$ 행렬의 n개의 고유벡터들이 기저벡터가 될 수 있다는 이야기이다. (basis vector의 기본 조건이 선형독립이다.)
고유벡터가 선형독립인 것은 서로 다른 n개의 고윳값을 가지고 있어야 하기 때문에 이는 곧 A가 서로 다른 n개의 고윳값을 가지고 있는 경우에, 행렬 $A$가 대각화가 가능하다는 이야기와 동일하다.
마지막으로 중요한 행렬에 대해 언급하고 이번 포스팅을 마치겠다.
먼저 'positive (semi) definite'이다.
Positive definite matrix (양의 정부호 행렬)

임의의 벡터 $x$에 대해 항상 위 부등식을 만족하는 행렬을 우리는 양의 정부호 행렬이라 부른다.
이 행렬들은 모든 고윳값이 항상 양수인 성질을 지니고 있다.
Positive semi-definite matrix는 양의 준정부호 행렬이라 하며 양의 정부호 정의에서 $=$가 들어가면 된다.
이 행렬은 모든 고윳값이 항상 음수가 아닌 성질을 지니고 있다.
우리는 역행렬이 존재하는 임의의 행렬 $B$에 대해 항상 positive definite matrix를 만들 수 있는데 $B^T B$를 만들면 된다.
$B^T B$는 항상 (symmetric) + positive definite matrix이다.
Symmetric matrix (대칭행렬)
이 행렬들은 모든 고유벡터가 서로 직교하게끔 대각화가 가능하다. 이를 스펙트럼 정리 (spectral theorem) 이라 한다.
고유벡터가 직교하는 것은 선형독립을 기본 전제로 하고 있으므로, 항상 대각화가 가능하며 $S^{-1} = S^T$이다.
이번 포스팅을 끝으로 선형대수학 기초개념 복습을 마치도록 하겠다.
다음 포스팅에서는 딥러닝에 필수적인 미적분학 / 확률통계 기초개념 복습을 하도록 하겠다.
'Deep dive into Deep learning' 카테고리의 다른 글
| Deep dive into Deep learning part 7 - Updated (0) | 2023.03.22 |
|---|---|
| Deep dive into Deep learning part 6. - Updated (0) | 2023.03.17 |
| Deep dive into Deep Learning Part 4. - Updated (0) | 2023.03.09 |
| Deep dive into Deep Learning Part 3. - Updated (0) | 2023.03.07 |
| Deep dive into deep learning part 2. - Updated (0) | 2023.03.05 |




댓글