"모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시길 바랍니다."
오늘은 지난 글에 이어 2차 미분 정보를 활용한 최적화, Second-order method 두 번째 글이다.
그 중 Hessian matrix를 이용한 Newton's method에 대해 살펴보고자 한다.
먼저 다음과 같은 optimization problem을 생각해보자.

표기를 최대한 simple하게 하기 위하여, 위와 같이 표현하였다.
여기서 θ는 파라미터이고 f(θ)는 objective function이다.
First-order optimizer는 위 f(θ)를 1차 근사한 함수를 최소화하는 방법으로 알고리즘을 유도하였다.
(물론, First-order talyor approximation은 직선이기 때문에 −∞로 최솟값을 구할 수 없기 때문에 θt와 θt+1 사이의 거리를 constraint하는 2차 꼴의 함수를 설정하였었다.)
기억이 나지 않는다면 아래 포스팅 글을 참고하기 바랍니다.
https://kyteris0624.tistory.com/20
Deep dive into optimization: Gradient descent (1)
"모바일 앱 환경에서는 latex이 깨져 나타나므로, 가급적 웹 환경에서 봐주시기 바랍니다.:)" 오늘부터 이제 본격적인 딥러닝 최적화 (Optimization)에 대한 이야기가 시작된다. 그 첫 번째 주제는 현
kyteris0624.tistory.com
그렇다면 Second-order method는 f(θ)를 2차 Taylor-approximation한 함수를 최소화하는 알고리즘이 아닐까?
미리 결론부터 말하자면 정답이다.
한 번 유도해보도록 하자.

위 수식은 f(θt+1)의 값을 2차 Taylor-approximation한 형태이다.
그렇다면 RHS (오른쪽 수식)를 최소화하기 위해서 미분을 하는데, θt+1에 대해서 미분하도록 하자.
(우변을 최소화하는 θt+1을 찾는 것이므로.)
미분한 식을 =0으로 두고 풀면 아래와 같이 식이 정리가 된다.

이것이 Newton's method 알고리즘이다.
물론, 실제 Practical algorithm은 H(θt)−1∇f(θt)에 step-size를 곱해주지만 여기선 편의상 생략한다.
결국 Hessian의 inverse에 gradient를 곱한 '방향'으로 파라미터 업데이트가 진행이 된다.
Second-order optimizer의 장점과 단점에 대해선 앞선 글에서 이야기를 하였으므로 본 글에서는 넘어가도록 하겠다.
다음 글을 참고하기 바란다.
https://kyteris0624.tistory.com/34
Deep dive into Opitmization : Second-order method (1)
"모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시기 바랍니다." 이번 포스팅 글부터는 2차 미분을 이용한 optimization algorithm에 대한 설명을 진행하고자 한다. 지난
kyteris0624.tistory.com
위에서 Hessian matrix를 'preconditioner'라고 하는데 gradient에 Preconditioner를 곱하는 것은 경사하강의 방향을 '보정'하기 위함이다. 결국 Preconditioning이 하는 것은 Loss surface의 geometry를 변경하는 것인데, (타원 -> 원) 이를 ill-conitioned problem을 완화시킨다고 표현하고, 그 결과 optimal point로의 수렴 속도가 더욱 빨라진다.
그리고 Hessian은 좋은 Preconditioner의 역할을 한다.

Preconditioner는 수치해석에서는 Quadratic form에서 Matrix의 condition number를 줄여주는 역할을 하고, 그 결과 타원의 모양을 원에 가깝게 바꿔주는 역할을 한다. Condition number는 Maximum eigenvalue와 Minimum eigenvalue의 비율이고, 이들이 줄어든다는 것은 결국 eigenvalue 사이의 차이가 줄어든다는 것이다.
이 점을 좀 더 자세하게 살펴보자. 이를 위하여 f(θ)를 다음과 같이 정의해보자.

θ에 대한 quadratic form의 일반적인 문제이다.
θ와 b는 vector이고, A는 symmetric positive-definite matirx라고 하자.
이를 최소화하기 위해 f(θ)를 미분하여 0이 되게 되는 값은 f′(θ)=Ax−b=0으로 Ax=b를 만족하는 x이다.
이때 A가 역행렬이 존재하는 행렬이면 x=A−1b가 된다.
하지만 만약 A matrix가 size가 매우 큰 행렬이면 어떻게 될까? 예를 들어 A∈R10000×10000이라면?
이 역행렬을 컴퓨터로 구하는데 시간이 오래 걸릴 것이다. 현재의 Neural network는 파라미터의 개수가 상당히 많은 overparameterized neural network이기 때문에 10000개보다 훨씬 더 많은 수천만/수억개 이상의 파라미터를 가지고 있다. 이 경우에는 역행렬을 구하는 것은 계산량이 상당히 클 것이다. (시간도 오래 걸릴 것이다.)
(non-convex problem은 차치하고서라도)
그리고 만약 A가 역행렬이 존재하지 않는 행렬이라면?
원래는 Pseudo-inverse matrix인 (ATA)−1AT를 계산해야 하지만 계산량이 매우 크다.
가장 쉽게 할 수 있는 방법은 A 행렬의 대각성분에 작은 값들을 더해주는 것인데 이렇게 할 경우 A 행렬이 역행렬이 존재할 수 있게 된다. 그렇지만 A 행렬이 성분의 조그만 변화에 영향을 크게 받는 행렬이라면, 이렇게 해서 역행렬을 구할 경우 원래 구했어야 하는 Pseudo-inverse matrix와 오차가 매우 클 것이다.
이 때, 입력의 조그만 변화에 영향을 크게 받는다는 것이 결국 A 행렬의 condition number가 매우 크다는 것이고, ill-condition matrix라는 것이다.
그렇다면 이러한 ill-conditioned problem을 완화하는 방법으로는 preconditioner matrix를 곱해주는 방법이 있고, 이 행렬을 M이라 해보자.
M−1Ax=M−1b로 문제가 바뀌었고, 이때 M−1A는 원래의 A행렬보다 condition number가 작은 행렬일 것이다. (물론, M이 좋은 preconditioner라는 전제 하에..)
위 문제를 수치적으로 푸는 것이 아닌, iterative algorithm으로 풀기 위해선 어떻게 해야 할까?
다음과 같이 하면 된다.
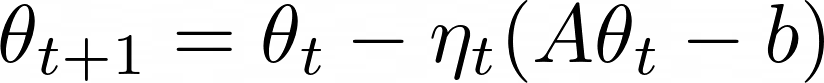
하지만 A가 ill-conditioned matrix라면 위 알고리즘에서 θt는 oscilliation 현상이 심하게 발생할 것이고,
이를 완화하기 위해서 Preconditioner matrix를 곱해줄 수 있을 것이다.
역시나 M−1A는 A보다 condition number가 작아졌다면, loss function은 원래의 타원 형태에서 원 형태에 더 가까워졌을 것이고 파라미터는 더욱 빠르게 optimal point로 수렴할 것이다.
Newton's method에 대해 정리하면 다음과 같다.
1. 파라미터 업데이트 방향을 결정할 때, 2차 미분 정보, 즉 curvature 정보를 반영하기 때문에 더 좋은 방향으로 이동한다.
2. Preconditioner로서 원래의 loss function의 condition number를 줄여주었기 떄문에 loss function의 모양이 원 형태에 더욱 가까워졌고, 이는 파라미터 업데이트 과정에서 oscilliation 현상을 완화하기 때문에 수렴 속도, 즉 convertgence rate이 더욱 빨라진다.
하지만, 지난 번에도 이야기하였듯 H−1을 계산하는 것은 상당히 계산량을 많이 요구하는 작업이고 요즘처럼 파라미터의 개수가 많은 모델들이 사용될 때는 더더욱 그러하다. 그리고 사실 Neural network에서 loss function은 non-convex하기 때문에 H−1은 positive (semi)-definite 하지도 않다.
(** 위에서 quadratic form에서 A를 positive definite이라고 가정하였었다. **)
그렇기 때문에 Newton's method는 saddle point problem을 지니고 있고 딥러닝에서 그 연산과 메모리 소모를 감수할만큼 실질적인 큰 장점을 누리기는 쉽지 않다.
(물론, Hessian 행렬 자체를 계산하는 방식은 계산량이 매우 크지만 Hessian-vector product를 계산하는 것은 약간의 트릭을 통해 효율적으로 가능하다. 이러한 수치연산 알고리즘을 활용하는 방식도 많이 있지만 본 글에선 다루지 않을 것이다.)
Hessian이 positive-(semi) definite 하지 않음을 보완하는 더 좋은 방법이 하나 있는데 그것은 Hessian matrix가 아닌 Fisher information matrix를 사용하는 것이다.
이를 Natural gradient descent 알고리즘이라고 하는데 다음에는 이에 대해서 살펴보도록 하자.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into Optimization : Second-order method (4) - Updated (2) | 2023.05.03 |
|---|---|
| Deep-dive into Optimization : Second-order method - Updated (0) | 2023.04.30 |
| Deep dive into Optimization: Second-order method - Updated (0) | 2023.04.19 |
| Deep dive into optimization : Adam - Updated (0) | 2023.04.12 |
| Deep dive into optimization : Adaptive step-size (1) - Updated (0) | 2023.04.06 |




댓글