모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시길 바랍니다.
이번 글과 다음 글에서는 Fisher information matrix를 활용한 알고리즘 'Natural gradient descent에 대해 이야기하고자 한다. 오늘은 Fisher information matrix를 설명하고, 다음 글에서는 이를 활용한 최적화 알고리즘 Natural gradient descent를 이야기하고자 한다.
* 본 내용은 Hogg 저. 'Introduction to mathematical statistics' 를 활용하였다.
우선, Fisher information matrix에 대해 알아보자.
여기서 말하는 'Fisher information' (피셔 정보) 란 무엇일까?
파라미터가 $\theta$인 pdf $f(x;\theta)$를 가진 확률변수 X를 생각해보자. 우리는 여기서 $\theta$에 대해 추정하고 싶은데, 우리가 가지고 있는 것은 위 확률변수에서 Sampling된 표본들이다. $i.i.d$하게 sampling 되었다고 가정하자.
그러면 Random sample $X_1, X_2, \cdots, X_n$ 모두 같은 pdf $f(x;\theta)$를 가질 것이다.
이 때 우리는 다음과 같은 함수 (Likelihood function)를 정의할 수 있다.

앞선 최적화 시리즈에서 $L$은 Loss fucntion (손실 함수)에 대한 표기였으나, 여기서는 우도 함수 (Likelihood function)를 의미한다.
이때 곱셈 연산을 우리는 합으로 바꾸어서 계산량을 줄일 수 있는데 이를 위해 $\log$를 취할 수 있다.
$\log$는 일대일 함수이므로 이를 사용하여도 된다.
그렇다면 Log-likelihood function은 다음과 같이 정의된다.

이 때 위 Log-likelihood function을 최대화하는 $\hat{\theta}$, 즉 $\theta$에 대한 추정값을 우리는 Maximum likelihood estimator (MLE)라 하고, 현재 내가 갖고 있는 데이터들을 sampling한 모집단의 분포, 정확히는 그 분포의 파라미터 $\theta$가 가질 수 있는 가장 그럴듯한 값을 나타낸다.
(여기서 파라미터 $\theta$는 예를 들어 모집단이 이항분포라면 성공 확률, 정규분포라면 $\theta$는 평균, 분산일 것이다.)
그렇다면 이 추정치가 얼마나 좋은지를 구분하는 기준, 나타내는 값은 무엇이 있을까?
첫 번째는 불편성 (Unbiasedness)이다. 정의는 다음과 같다.
Random variable $X$의 pdf $f(x;\theta)$에서 i.i.d 하게 sampling된 표본 $X_1, \cdots, X_N$이 있을 때, 이들의 통계량 $T = T(X_1, \cdots, X_N)$이 다음을 만족할 때 $T$를 $\theta$에 대한 불편추정량이라고 한다.
$\mathbb{E}(T) = \theta$
다음으로 위 불편추정치 통계량도 확률변수이기 때문에 분산을 가지고 있을 것이다. 즉, 평균 (참값)으로부터 떨어진 정도의 기댓값, 분산이 작으면 작을 수록 좋은데 이 분산이 한없이 작아질 수는 없다. (즉, 완전히 0이 될 수는 없다.)
적절한 양수의 Lower bound, 즉 분산 하한을 가진다는 것이 알려져 있는데 이를 우리는 'Rao-Cramer lower bound'라고 한다.
이 라오-크라메르 하한 부등식에서 나오는 것이 피셔 정보이다.
먼저, 라오-크라메르 하한부터 이야기하자.
Random variable $X$의 pdf $f(x;\theta)$에서 i.i.d하게 sampling된 표본 $X_1, \cdots, X_N$이 있을 때, 이들의 통계량 $Y = u(X_1, \cdots, X_N)$이 있다고 하자. $Y$가 $\theta$의 불편추정량일 때, $Y$의 분산은 다음 부등식을 만족한다.
$Var(Y) \ge \frac{1}{n I(\theta)}$
이 때, $I(\theta)$가 Fisher information을 의미한다.
그리고 분산이 Rao-cramer lower bound일 때 통계량 $Y$는 $\theta$의 efficient estimator (효율 추정량)이라고 한다.
위 식에 대해 직관적으로 이해해보자. 통계량 $Y$는 당연히 분산이 작을수록 좋다. 그렇다면 분모에 있는 피셔 정보가 클수록, 분산은 작아지므로 우리가 갖고 있는 통계량 $Y$가 참 파라미터 $\theta$에 대해 큰 피셔 정보값을 가지고 있을 수록 더 좋은 통계량/추정치 (estimator)라는 의미가 된다. 즉, 우리가 갖고 있는 데이터 (Sample)들이 얼마나 파라미터에 대해 정보를 제공해주는가? 를 정량적으로 측정해주는 값이 Fisher information이 된다.
자 그러면 피셔 정보를 유도해보자.
다음과 같은 항등식으로 시작할 수 있다.

이를 $\theta$에 대해 미분하면

이는 다음과 같이 표현할 수 있다.

로그 미분법을 적용하면 위와 아래의 등식이 동일함을 알 수 있다.
이 식을 기댓값으로 표현하면, $\mathbb{E}[\frac{\partial \log f(X;\theta)}{\partial \theta}] = 0$이므로 확률변수 $\frac{\partial \log f(X;\theta)}{\partial \theta}$의 기댓값은 0임을 알 수 있다. (이는 공식 유도에 종종 쓰이는 중요한 성질이다.)
위 식을 한 번 더 미분하면,

위와 같이 나온다.
이 중 오른쪽 두 번째 항을 기댓값으로 표현한 것이 바로 Fisher information이 된다.

또한, 위 마지막 항등식을 이용해서 Fisher information은 다음과 같이 볼 수도 있다.

즉, 피셔 정보는 확률 변수 $\frac{\partial \log f(X;\theta)}{\partial \theta}$의 분산이다.
피셔 정보는 통계학에서는 주어진 데이터가 파라미터에 대해 얼마나 정보를 제공하는가를 나타내는 값이고,
머신러닝에서는 optimization algorithms, 또는 Neural network 파라미터의 성질 등을 분석할 때 자주 등장하는 값이다.
(Neural network에서 Negative log-likelihood를 loss function으로 많이 사용함을 떠올려보자.)
만약 $\theta$가 벡터라면 위 피셔 정보는 행렬이 될 것이고, 이를 우리는 Fisher-information matrix라고 부른다.
이때 log-likelihood의 gradient, 즉 확률변수 $\frac{\partial \log f(X;\theta)}{\partial \theta}$를 score function이라고도 부르고 결국 피셔 정보 (행렬)은 위 score function의 (공)분산이자 동시에 한 번 더 미분한 것의 Expectation이 된다.
여기서 (공)분산이 결국 Negative log-likelihood의 Second-moment, 즉 이차 미분과 동일한데, 그렇기 때문에 Fisher inforamtion은 Hessian과 많이 엮어지면서 동시에 해당 loss function의 Curvature 정보를 나타낸다고 볼 수 있다.
(loss function이 Negative log-likelihood인 경우에)
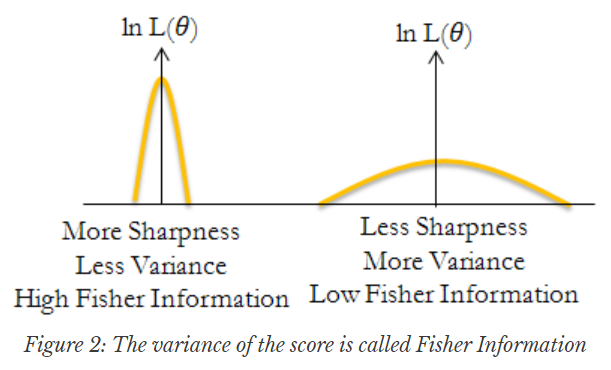
이것은 앞서 이야기한 Newton's method에서 Hessian을 쓰는 것과 Motivation이 비슷한데 gradient (1차 미분 정보)만 이용하는 것이 아니라 Curvature (2차 미분 정보)도 함께 활용할 수 있는 optimization algorithm과 이어지게 한다.
그리고 이것이 바로 Natural gradient descent라고 한다.
마지막으로 Fisher는 KL-divergence와도 깊은 연관성이 있는데 두 확률분포 $p(X;\theta)$와 $p(X;\theta')$이 있을 때, $\theta$와 $\theta'$의 차이가 크지 않다면 두 확률분포 사이의 차이를 KL-divergence로 측정할 때, 이는 Fisher와 연결될 수 있다. 즉, 다음이 성립한다. 이에 대한 증명은 매우 심플하고 KL-divergence 정의에 약간의 Taylor approximation을 사용하여 대입하면 쉽게 유도되기 때문에 넘어가겠다.

위 성질은 다음 글 Natural gradient descent에 대한 설명에서도 활용되어지므로, 알고 넘어가자.
Natural gradient descent는 이론적으로 매우 훌륭한 알고리즘이다. 다음 글에서 이에 대해 이야기하겠다.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into Optimization : Second-order method (5) - Updated (0) | 2023.05.06 |
|---|---|
| Deep dive into Optimization : Second-order method (4) - Updated (2) | 2023.05.03 |
| Deep dive into Optimization: Second-order method - Updated (0) | 2023.04.25 |
| Deep dive into Optimization: Second-order method - Updated (0) | 2023.04.19 |
| Deep dive into optimization : Adam - Updated (0) | 2023.04.12 |




댓글