모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시길 바랍니다.
그동안 우리는 Gradient descent부터 시작하여, Momentum, Adam 등의 딥러닝에서 많이 쓰이는 First-order optimizer와 Newton's method, Natural gradient descent 두 대표적인 Second-order optimizer를 다뤄왔다.
이제 본 포스팅의 메인 주제인 'Convex optimization'으로 다시 돌아가자.
https://kyteris0624.tistory.com/18
Deep dive into optimization: Convexity
"모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 pc 웹 환경에서 읽어주시기 바랍니다." "What is the convex?" 오늘은 최적화 개념 중 매우 중요하면서 가장 기본이 되는 개념인 convexity에
kyteris0624.tistory.com
위 글에서 우리는 아주 기본적인 convexity의 정의에 대해서 다루었다.
(추가적으로 smoothness, strong-convex의 정의에 대해서도 다루었고 이 둘도 매우 중요하다.)
하지만 Convex optimization이라는 (응용 수학) 분야에서 이야기하는 Convexity와 관련된 내용들은 위의 내용보다 훨씬 많고 그 내용들 이 학문을 공부하는데 있어 중요한 의미들이 있다.
다시 한번 Convex optimization problem이 무엇인지 떠올려보자.

$f$의 Domain이 $C \subset \mathbb{R}^n$이 convex set이고, 함수 $f(x)$가 convex function일 때 우리는 위 문제를 'convex optimization problem'이라 부른다.
우리가 그동안 배워온 First-order optimizer, Second-order optimizer는 모두 위 문제를 iterative algorithm으로 푸는 방법들이었다. (물론 Neural network의 loss function은 non-convex하지만..)
Convex function의 가장 중요한 특징 중 하나는 'Global minima = Local minima'라는 사실이다.
그리고 위와 같은 solution이 만족해야만 하는 특정한 제약조건이 없는 문제를 Unconstrained optimization problem이라 부른다.
Convex constrained optimization problem은 다음과 같다.
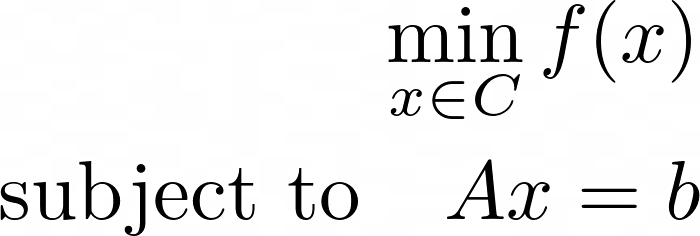

똑같이 $f(x)$를 Minimize하는 문제이지만 $x$가 convex set의 원소이여야 하며, 우리가 찾는 optimal solution (또는 set)이 $Ax = b$ 또는 $Ax \le b$를 만족해야 하는 제약 조건이 존재하는 것이다.
다음 글에서는 convex optimization의 꽃이라고 불리우는 'Duality'에 대한 이야기를 시작할 것이다.
오늘은 그 Duality를 이해하는데 기초가 되는 여러 개념들을 이야기하고 마무리하도록 하겠다.
* Norms
Norm은 일반적으로 inner product로 정의되는 함수이다.
내적 공간 $V$의 inner product는 다음과 같은 함수이다.
$x, y, z \in V$에 대해서, $\langle x, y \rangle : V \rightarrow \mathbb{R}$이면서 다음과 같은 조건을 만족한다.
$1 \langle x, x \rangle \ge 0$
$2 \langle x, y \rangle = \langle y, x \rangle$
3. $a, b \in \mathbb{R}$에 대하여, $\langle ax + bz, y \rangle = a \langle x, y \rangle + b \langle z, y \rangle$
대표적으로 위 정의를 만족하는 내적은 $\langle x, y \rangle = x^T M y$가 있다. 이때 $M$은 symmetric positive-definite matrix이다.
우리가 많이 쓰는 "dot product"는 위에서 $M = I$, 즉 Identity matrix인 경우이다.
Norm은 다음과 같이 정의된다.
$\lVert x \rVert = \sqrt{\langle x, x, \rangle}$.
즉, 우리는 벡터의 크기를 norm을 통해서 정의하는데 이 norm은 내적을 통해서 정의된다. 내적이란 결국 벡터공간에 기하학적 성질들을 부여해주는 함수이다. (벡터의 크기, 두 벡터 사이의 거리, 두 벡터 사이의 각도 etc)
가장 대표적인 norm은 $\mathbb{R}^n$에서 쓰이는 $L_1$-norm, $L_2$-norm, $L_{\infty}$-norm이 있다.
$L_1$-norm은 다음과 같이 정의된다. $\lVert x \rVert_1 := |x_1| + |x_2| + \cdots |x_d|$.
이 중 $L_2$-norm이 Euclidean norm이라고도 부른다. $\lVert x \rVert_2 = \sqrt{\sum_{i=1}^d x_i^2}$.
$L_{\infty}$-norm은 $\max_{i} |x_i|$이다.
convex optimization의 관점에서 norm도 convex function이다. (즉, convex의 정의를 만족한다.)
* $\ell_p$ norm

이 때, $p \ge 1$을 만족한다.
우리가 흔히 봐왔던 $\ell_1 norm$, $\ell_2 norm$, $\ell_{\infty}$ norm은 위 equality에 $p$에 $1, 2, \infty$를 대입하면 유도가 된다.
* Cauchy-Schwartz and Holder Inequalities
Cauchy-Schwartz inequality는 inner product이 $\ell_2$ norm에 upper bound함을 보여주는 inequality이다.

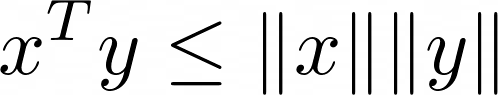
위 부등식은 매우 자주 등장하는 중요한 부등식이다.
위 부등식을 일반화한 것이 Holder inequality이고 다음과 같다.

Cauchy-schwartz는 $p=q=2$인 경우이고, $p=1, q= \infty$일 때도 위 inequality를 만족한다.
Dual norm은 Dual vector space에 정의된 norm이다.
Dual vector space의 정의는 다음과 같다.
벡터공간 $V$에서 $\mathbb{R}$로 사상하는 선형 변환 (linear transformation)을 우리는 선형 범함수 (linear functional)이라고 한다.
이 선형 범함수의 집합을 Dual vector space라고 하고, 이름에서 알 수 있듯이 이 공간도 '벡터 공간'이다.
즉, 벡터 공간으로서의 공리적 정의를 모두 만족한다.
(사실 선형변환의 집합 자체가 벡터 공간이 되기 때문에 선형변환의 한 종류인 선형범함수의 집합도 벡터공간이 되는 것은 자명하다.)
이 공간을 보통 $V^{\star}$라고 많이 표기한다. 이 공간은 $V$와 대응되는 Dual space로서 차원이 같고 (즉, 동치 관계) 같은 내적 함수가 정의되어져 있다.
다만, norm에 있어서는 다른 형태의 norm을 쓰는데 이를 dual norm이라고 한다.
만약 $V$에서 $L_p$-norm을 사용한다면, $V^{\star}$에서는 $L_q$-norm을 사용하고 이때, $\frac{1}{p} + \frac{1}{q} = 1$이다.
이 때, $\lVert \cdot \rVert_q$는 $\lVert \cdot \rVert_p$의 dual norm이라고 부른다.
dual norm의 일반적인 정의는 다음과 같고 $\lVert \cdot \rVert_*$로 표기한다.

Dual norm에 대해서는 다음 글에서 좀 더 자세히 설명하겠다.
다음은 convex function의 몇 가지 성질들이다.
* epigraph
함수 $f$의 epigraph는 다음과 같이 정의된다.

함수 $f$가 convex라면, epi $f$도 convex하고, epi $f$가 convex하면 함수 $f$도 convex하다.
즉, 필요충분관계이다.
* Conjugate function
Conjugate function의 중요성은 convex optimization 에서 매우 크다. 이는 추후 따로 자세히 다룰 예정이고 지금은 정의만 봐두자.
함수 $f$의 conjugate function은 다음과 같이 정의된다.

다른 말로는 Fenchel conjugate, Legendre-Fenchel transform이라고도 한다.
$f$가 convex하면, $f^*$도 convex하고, $f^{**} = f$이다.
이 때, $f^{**}$를 bi-conjugate이라고도 한다.
마지막으로 convex function, smoothness, strong-convex의 equivalent conditions에 대해서는 다음 pdf를 첨부하도록 하겠다.
1페이지는 특히 한 번 꼭 보도록 하자.
* chrome-extension://efaidnbmnnnibpcajpcglclefindmkaj/https://www.cs.ubc.ca/~schmidtm/Courses/Notes/convex.pdf
이상으로 "Duality"를 설명하는데 필요한 배경지식을 마치도록 하겠다.
다음 글에서 본격적으로 Duality를 들어가보도록 하자.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into Optimization : Duality (2) -Updated (0) | 2023.05.18 |
|---|---|
| Deep dive into optimization : Duality (1) - Updated (1) | 2023.05.14 |
| Deep dive into Optimization : Second-order method (5) - Updated (0) | 2023.05.06 |
| Deep dive into Optimization : Second-order method (4) - Updated (2) | 2023.05.03 |
| Deep-dive into Optimization : Second-order method - Updated (0) | 2023.04.30 |




댓글