모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시길 바랍니다.
* 본 글은 skip하여도 괜찮습니다.
오늘은 Natural gradient descent 두 번째 글이다. 첫 번째 글은 아래 링크 참조하기 바란다.
https://kyteris0624.tistory.com/41
Deep dive into Optimization : Second-order method (4)
모바일 앱 환경에서는 latex 수식이 깨져 나타나므로, 가급적 웹 환경에서 봐주시길 바랍니다. 오늘과 다음 글 두 번에 걸쳐 Natural gradient descent에 대해 이야기하고자 한다. Natural gradient descent는 Fis
kyteris0624.tistory.com

앞선 글에서 Fisher information matix에 대해 설명하면서 위의 정의를 이야기하였다.
우선 Fisher information matirx는 정의 자체에서 볼 수 있듯이 score vector ($\nabla \log p(x, y|\theta)$)의 Tensor product로 이뤄져 있기 때문에 Symmetric and Positive Semi-definite이다.
(Hessian matrix는 symmetric하지만 PSD는 보장되지 않는다.)
위와 같은 Fisher를 우리는 practical한 상황에서 approximation을 시켜서 사용하는데 가장 대표적인 근사 행렬로는 'Empirical Fisher'가 있다. data distribution (또는 model distribution) $P_{x, y}$가 아닌, target (label) distribution을 사용하는 것이고 그것은 다음과 같이 표현될 수 있다.
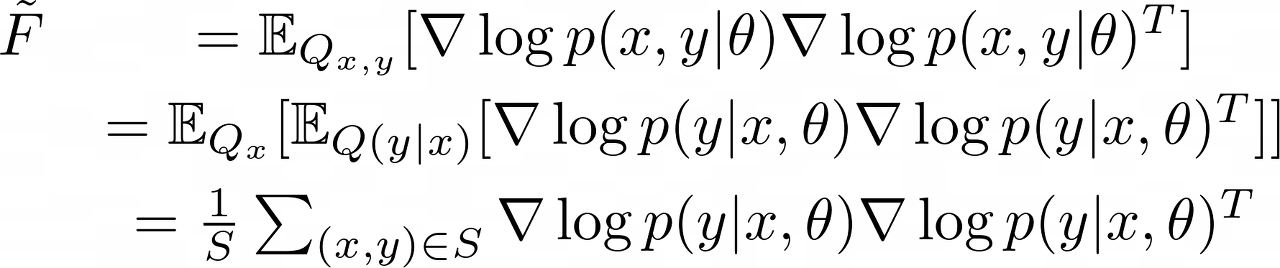
Empirical Fisher 또한 Fisher와 마찬가지로 PSD이다.
그리고 우리는 어차피 gradient를 계산하기 때문에 위 Empirical Fisher는 계산량이 크지 않다.
또한 Empirical Fisher는 Fisher와 비교했을 때, rank가 작기 때문에 diagonal, block matrix 같은 성분 , 부분행렬을 계산하는 것이 더 쉽다. (계산량이 더 적다)
* 이 부분은 이해가 잘 안 되면 그냥 넘어가도 괜찮다.
그 이유는 Fisher matrix는 정의에서 알 수 있듯이 'data (true) distribution'을 활용해서 계산되지만, Empirical Fisher는 sampling된 유한한 개수의 (finite) data를 활용해서 계산이 이뤄진다. rank가 작다는 것은 결국 linearly independent한 column/row vector의 개수가 적다는 것이고, column vector / row vector 사이의 'linear dependencies'가 존재한다는 것이다. 즉, 일부 column vector (row vector)는 다른 vector들의 linear combination으로 표현이 된다는 것이고, 이 말은 'redundant' information을 담고 있다는 것이다.
그리고 그 이유는 곧 Empirical Fisher는 finite sample를 이용해서 계산이 되기 때문에 결국 data의 기저에 있는 (true distribution)을 온전히 담아낼 수 없다. 이러한 limitation이 결국 row vector , column vector의 linear dependency를 초래하는 반면, Fisher는 true distribution을 알고 있기 때문에 불필요한 column/row vector가 훨씬 적을 수밖에 없다.
또한, numerical method에서 lower rank일수록 matrix factorization 계산이 좀 더 편하고, matrix를 활용한 연산이 더욱 편하긴 하다. (즉, memory , time complexity가 작아진다.)
* 여기까지
하지만, Empirical Fisher가 아닌 Fisher를 쓸 때 장점도 있는데 가장 대표적으로 Fisher는 아주 좋은 Hessian의 approximation/substitute가 될 수 있기 때문이다. (loss function이 Negative log-likelihood인 경우)
그러나 이 성질은 Empirical Fisher에서는 보장되지 않는다.
그리고 Empirical Fisher도 Fisher처럼 항상 inverse matrix가 존재하는 것이 항상 보장되는 것은 아니기 때문에 역행렬을 근사해서 구할 때, 원치 않는 bias/error가 생길 수 있고 이 또한 performance의 문제가 될 수 있다.
이걸로 Second-order method에 대한 설명을 마무리하겠다.
'Deep dive into Optimization' 카테고리의 다른 글
| Deep dive into optimization : Duality (1) - Updated (1) | 2023.05.14 |
|---|---|
| Deep dive into optimization : Convex optimization (Updated) (0) | 2023.05.09 |
| Deep dive into Optimization : Second-order method (4) - Updated (2) | 2023.05.03 |
| Deep-dive into Optimization : Second-order method - Updated (0) | 2023.04.30 |
| Deep dive into Optimization: Second-order method - Updated (0) | 2023.04.25 |




댓글