모바일 앱 환경에서는 LATEX 수식이 깨져 나타나므로 가급적 웹 환경에서 봐주시길 바랍니다.
오늘은 RNN의 구조와 내부 연산들에 대해 알아보도록 하자.
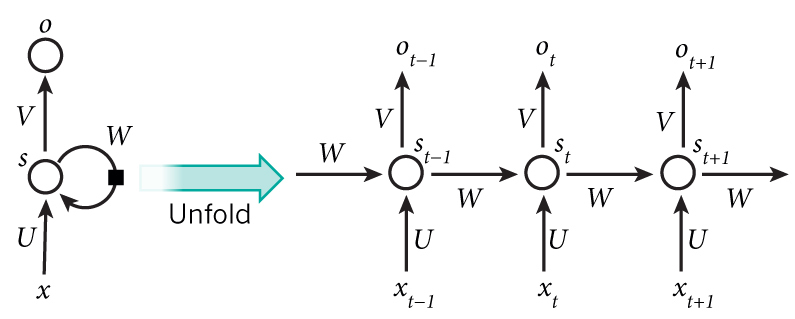
Recurrent Neural network (RNN)는 위 구조처럼 Hidden node가 방향을 가진 edge로 연결돼 순환구조를 이루고 있다.
우측 그림을 통해 살펴보자.
$x_{t-1}, x_t, x_{t+1}$은 시점 $t-1, t, t+1$에 들어오는 input이다. RNN은 음성, 문자처럼 순서가 있는 데이터 (sequential data) 처리에 능숙한데 그 이유는 위와 같이 시간 순서에 따라 들어오는 데이터를 순차적으로 처리할 수 있기 때문이다.
$t$ 시점에 데이터 $x_{t}$가 들어오면 이것은 matrix $U$를 통해 hidden node (hidden state) $s_{t}$의 input으로 들어간다. 그리고 이전 시점 ($t - 1$)의 hidden state인 $s_{t-1}$이 matrix $W$를 거쳐서 hidden state $s_t$의 input으로 들어간다. 그리고 여기서 activation function ($\sigma(\dot))을 거치면 그것이 hidden state의 output이 된다.
즉, 다음과 같이 수식으로 표현된다.
$s_t = \sigma(Ws_{t-1} + Ux_t)$이고, $t$ 시점의 output $o_t$는 $V s_t$
위 연산을 통해서 알 수 있는 것은 $s_t$에는 이전 상태 (시점)까지의 모든 데이터들의 특징이 존재한다.
그래서 위와 같은 hidden node를 memory cell이라고도 부른다.
여기서 $W, U, V$ 세 종류의 matrix가 parameter들이고 이들이 backpropgation을 통해서 학습이 진행된다.
또한 모든 state $t$는 동일한 파라미터를 사용하는 shared weights 구조이다.
하지만 이러한 RNN의 문제점은 무엇일까?
RNN의 backpropagation은 forrwad pass와 동일하게 시간 방향으로 이뤄지며 위 그림을 예시로 들면, $t+1$ 시점에서 $t-1$시점으로 거꾸로 역전파가 수행이 될 것이다. (forward는 $t-1$에서 $t+1$ 시간 순서로 흘렀음을 기억하자)
이를 계산 그래프 (computational graph)로 표현하면 다음과 같다.

이러한 RNN계열의 backpropagation을 Backpropagation Through Time (BPTT) 라고 하는데, 당연히 데이터의 크기가 커질수록, 즉 시간 크기가 커질수록 오래된 데이터에 대해서는 backpropagation이 잘 이뤄지지 않을 것이다.
gradient가 누적되어 곱해지면서 점점 작아지는 현상이 발생하는 것인데, 이를 우리는 앞에서 gradient vanishing problem이라 하였다. RNN은 과거 방향으로 gradient가 전파되면서 $x_{t-1}, x_t, x_{t+1}$ 사이의 의존 관계를 학습할 수 있는데, 이렇게 gradient vanishing 현상이 발생하면 이들 사이의 관련성을 학습하기 힘들어진다.
이를 해결하기 위해서 나온 모델이 대표적으로 Long-Short term Memory (LSTM) , Gated Recurrent Unit (GRU)가 있다.
LSTM을 시각화한 그림은 다음과 같다.
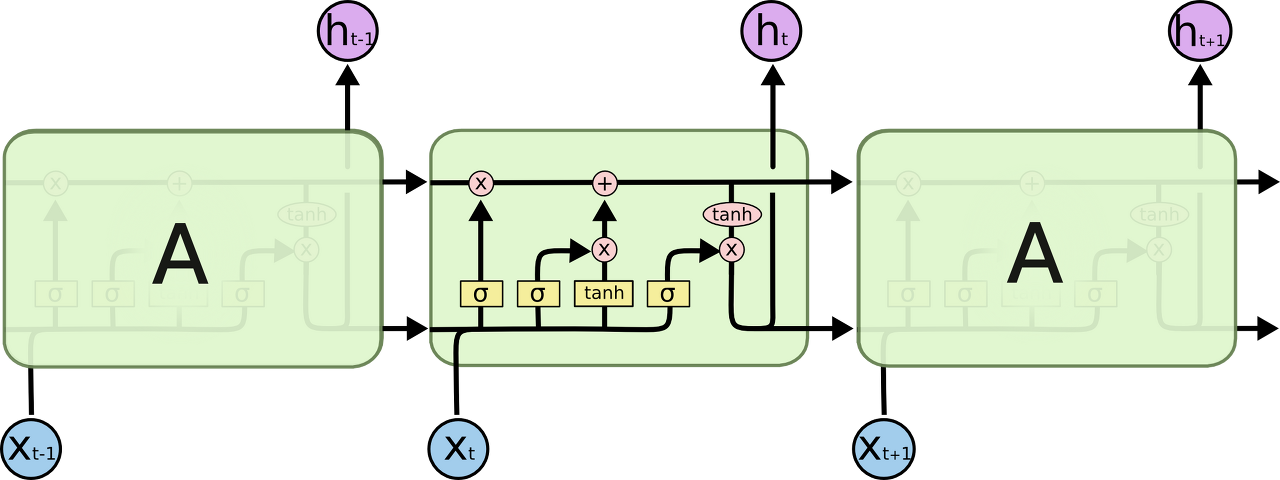
하나의 cell (hidden state)에서 이뤄지는 연산을 시각화한것으로서 그림만 보면 복잡해보이지만 실제로는 그렇게 복잡하지 않다.
결국 LSTM의 핵심은 과거 시점 $t-1$에서 정보를 받아 현재 시점 $t$에서 다음 시점 $t+1$로 정보를 전달할 때, 무엇을
'망각'할지, 무엇을 '추가'할지 처리하는 기능이 추가된 것이다.
기존 RNN은 과거 hidden state의 정보를 모두 받고 현재 hidden state의 정보를 모두 활용하여 연산하고, 이들을 다음 hidden state로 전달하였는데, LSTM에서는 이렇게 처리하지 않고, 과거 정보에서 일부는 '망각'하고 현재 정보에서 일부를 '추가'하여 다음 시점으로 전달하는 방식을 활용한다.
이 '망각'과 '추가'를 처리해주는 함수가 위 그림에서 $\sigma$ 즉 sigmoid function이다.

Sigmoid output은 $0$과 $1$사이로서 얼마만큼의 정보를 보존할지를 이 값을 통해 결정한다.
만약에 $1$이 나온다면 모든 정보를 보존하는 것이고 (즉 아무런 정보도 망각하지 않는 것), $0$이 나온다면 모든 정보를 망각하는 것이다.
LSTM에서 이뤄지는 연산은 다음과 같다.
1. 우선, 새로운 정보 $x_t$가 들어왔을 때, 이전 hidden state에서 들어온 정보에서 얼마만큼을 망각할지 결정한다.
$f_t = \sigma(W_f \dot [h_{t-1}, x_t])$
2. 그리고 현재 cell에는 얼마만큼의 정보를 저장할지 결정하는 연산, 현재 cell에 들어온 정보에 대한 연산을 수행한다.
$i_t = \sigma(W_i \dot [h_{t-1}, x_t])$
$\tilde{C}_t = tanh(W_c \dot[h_{t-1}, x_t])$
3. 이제 $C_{t-1}$을 C_t로 업데이트하는 연산을 수행한다.
$C_t = f_t \times C_{t-1} + i_t \times \tilde{C_t}$
위 연산을 보면 이전 cell $C_{t-1}$에 대해서 $f_t$를 통해 얼마만큼은 망각할지 결정되고, 현재 들어온 정보를 얼마만큼 활용하여 $C_t$라는 새로운 cell state로 업데이트를 진행함을 알 수 있다.
현재 cell state에서의 output $o_t$는 다음과 같이 연산이 수행된다.
$o_t = \sigma(W_o [h_{t-1}, x_t])$
$h_t = o_t \times tanh(C_t)$
'Deep dive into Deep learning' 카테고리의 다른 글
| Deep dive into Deep learning part 24 : RNN(5) (1) | 2023.06.16 |
|---|---|
| Deep dive into Deep learning part 23 : RNN (4) (1) | 2023.06.04 |
| Deep dive into Deep learning part 21 : RNN (2) (0) | 2023.05.26 |
| Deep dive into Deep learning part 20 : RNN (1) (0) | 2023.05.20 |
| Deep dive into Deep learning part 19 : Regularization(4) - Updated (2) | 2023.05.16 |




댓글