*** 모바일 앱 환경에서는 latex 수식이 깨져서 나타나므로, 가급적 웹 환경에서 읽어주시길 바랍니다 :) ***
"Linear algebra, Probability and Statistics, Calculus review"
앞으로 3개의 포스팅에서는 선형대수학, 확률과 통계, (벡터) 미적분학에서 딥러닝에 필수적인 최소한의 내용을 복습하고자 한다.
오늘은 선형대수학에 대한 기본 개념 요약글을 올리겠다. (선형대수학 2개 + 확통 / 미적분학 1개 포스팅 예정)
딥러닝에서 위 수학들은 기초 중에 기초이기 때문에 반드시 잘 알고 넘어가야 한다.
<선형대수학 Linear algebra>
먼저 "선형성" 이란 무엇인지 복습하자.
함수 $f$에 대하여,
1. 가산성 (Additivity) : 임의의 $x, y$에 대하여, $f(x+y) = f(x) + f(y)$
2. 동치성 (Homogeneity) : 임의의 실수 $\alpha$에 대하여, $f(\alpha x) = \alpha f(x)$
위 두 성질이 항상 성립할 때 함수 $f$는 선형적이라고 한다.
대표적인 선형성을 만족하는 함수가 행렬 (Matrix) 이다.
다음으로 스칼라, 벡터, 행렬, 텐서에 대해 정리하자.

Scalars (스칼라) 는 수이다. 자연수, 정수, 실수 등이 모두 스칼라에 포함된다.
Vector(벡터)는 스칼라들의 1차원 배열 (1D-array)이다. 위 예시에서의 벡터는 총 3개의 성분을 가지고 있다.
선형대수학에서는 '벡터공간' (Vector space over a field) 을 먼저 정의하고, 이에 대한 원소를 벡터라 한다.
이때 field는 특정한 연산체계/성질들이 정의된 구조로서, 대표적으로 $\mathbb{R}$, $\mathbb{C}$가 field이다.
그리고 field의 원소를 우리는 스칼라라고 한다.
가장 대표적인 벡터공간은 $\mathbb{R}^n$이고, 이를 우리는 유클리드 공간이라 한다.
위 예시에서의 벡터는 성분이 3개 있으므로, $\mathbb{R}^3$의 원소이다.
그리고 '열벡터' (Column vector) 꼴로 표현하는 것이 일반적이다.
Matrix (행렬)은 스칼라들의 2차원 배열 (2D -array)이다. 이때 가로축을 '행' (Row), 세로축을 '열' (Column)이라고 표현하며 위 예시에서의 행렬은 3행 2열이다.
수학에서는 행렬 $A$가 $R^{3 * 2}$의 원소라고 표현한다.
또한, 행렬은 벡터들의 배열이라고 볼 수도 있다. 즉, 위 행렬은 열벡터 [1, 3, 5]와 열벡터 [2, 4, 6]의 배열로 볼 수 있다.
행렬을 열벡터의 배열 (또는 행벡터의 배열)로 보는 것은 선형대수학을 더 깊이 이해하는데 도움이 된다.
그리고 선형대수학에서 행렬의 역할과 기능은 '선형사상' 에 있다. 선형사상이란 위에서 언급한 가산성, 동치성을 만족하는 사상 (map)을 의미하고, 행렬은 그 성질을 만족한다.
즉, 임의의 행렬 $A$는 임의의 벡터 $x, y$에 대해, $A(x+ y) = Ax + Ay$, $A(cx) = c Ax$이다. (단, $c \in \mathbb{R}$)
하나의 벡터공간 $\mathbb{R}^m$에서 다른 벡터공간 $\mathbb{R}^n$으로 mapping해주는 대표적인 선형변환은 행렬 $\mathbb{R}^{n \times m}$이다.
마지막으로 그 이상 차원을 가진 배열들을 우리는 Tensor (텐서)라고 표현한다.
텐서는 배열을 일반화하여 표현한 것으로 0차원 텐서를 스칼라, 1차원 텐서를 벡터, 2차원 텐서를 행렬이라고 볼 수도 있다.
다음으로 벡터와 행렬의 기본적인 연산에 대해 알아보자.
가장 기본적인 연산 덧셈 / 뺄셈 / 실수배는 모두 'element-wise operation'이다. 여기서 'element-wise operation'이란 성분별로 덧셈 / 뺄셈 / 실수배를 수행한다는 이야기이다.



벡터와 행렬의 덧셈, 뺄셈은 각 대응되는 원소별로 연산이 진행되기 때문에 원소의 개수와 모양이 같아야 덧셈, 뺄셈을 정의할 수 있다. 즉, 3행 2열 행렬과 2행 3열 행렬은 덧셈, 뺄셈이 불가하다는 것이다.
또, 성분의 개수가 2개인 벡터와 3개인 벡터는 덧셈, 뺄셈이 불가하다.
그렇다면 이제 곱셈은 어떻게 정의할까?
벡터, 행렬의 곱셈은 일반적인 실수 체계에서의 곱셈과는 다르기 때문에 별도의 정의 방법이 있다.
벡터에서는 '내적', '외적' (Dot product / Inner product, Outer product) 연산이 있다.
엄밀하게 이야기해서 내적 (Inner product)보다 점곱 (dot product)이 더 넓은 개념인데, 본 포스팅에서는 둘을 동일하게 취급한다.
내적 (inner product) 의 정의는 다음과 같다.
$\langle \cdot, \cdot \rangle : V \times V \rightarrow \mathbb{R}$이며, 다음을 만족해야 한다.
1. $x, y, z \in V$, $a, b \in \mathbb{R}$에 대해,
$\langle x, y \rangle = \langle y, x \rangle$
2. $\langle ax + by, z \rangle = a \langle x, z \rangle + b \langle y, z \rangle$
3. $\langle x, x \rangle \ge 0$ ($0$인 경우는 $x = 0$인 경우밖에 없다.)
본 글에서는 위 inner product는 dot product만 취급하겠다.
내적은 본질적으로, 벡터공간에 '기하학적 성질'을 부여해주는 함수이다. 즉, 벡터공간에 내적을 정의함으로서 우리는 '벡터의 크기', '벡터 사이의 각도' (특히, 직교) 등을 정의할 수 있다.
그리고 이 정의는 '내적'에 의존한다. 그렇기 때문에 내적을 어떻게 정의하냐는 해당 벡터공간의 기하학적 성질을 바꿔주는 는 매우 큰 함의가 있다.
다만 본 글은 '기초적인 내용'에 대한 정리글이므로 그냥 유클리드 내적, dot product만 고려하도록 하겠다.

자 결국 각각 대응되는 성분끼리 곱하고 더한 것이다.
구체적인 예시를 보면 더욱 잘 와닿는다.

이 때 두 벡터 ($a$, $b$)의 내적을 $a \cdot b$라고 표현하기도 하지만 $a^T b$로도 표현한다.
이때 $T$라는 것이 붙었는데 이는 Transpose (전치)의 앞글자에서 따온 것이다.
전치 연산은 텐서에 적용되는 특수한 연산인데 매우 단순하다.
벡터의 전치는 열벡터를 행벡터로 바꿔 표현하는 것이고, 행렬의 전치는 주대각선을 바탕으로 서로 대칭이동시키는 것이다. (사실, 행렬의 전치는 duality와도 연결되는 중요한 함의가 있다.)
역시나 예시를 들면 쉽게 이해된다.


행렬의 전치는 열벡터를 행벡터로, 행벡터를 열벡터로 전치시킨 것으로 이해하면 더욱 잘 와닿는다. (이것이 벡터의 전치이다.)
또한, 벡터의 덧셈, 뺄셈, 내적 모두 '교환법칙'이 성립한다.
벡터의 외적은 내적과 정반대이다. $u \otimes v = u v^T$이다.
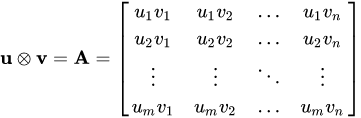
역시나 내적과 외적 모두 두 벡터의 성분의 개수 (차원의 크기)가 같아야 정의된다는 것을 쉽게 알 수 있다.
또한, 내적은 연산 결과 스칼라값이 나오는 반면, 벡터의 외적은 연산 결과 행렬이 나온다.
위 행렬은 아주 중요한 성질이 있는데 뒤에서 이야기하도록 하겠다.
행렬의 곱셈은 어떻게 정의될까? 행렬의 곱셈은 조금 특수하다.
행렬의 곱셈은 크게 두 가지 방법으로 해석되어질 수 있다.
1. 벡터의 내적
앞에서 행렬은 열벡터의 배열 (또는 행벡터의 배열)로 볼 수 있다고 하였다. 그렇다면 두 행렬 $A$와 $B$의 곱셈은 $A$ 행렬의 행벡터와 $B$행렬의 열벡터의 내적으로 볼 수 있다.
가장 단순한 2행 2열짜리 행렬 2개의 곱셈으로 예시를 들어보겠다.

앞에 행렬의 행벡터와 뒤의 행렬의 열벡터의 내적을 수행한다.
이때 앞의 행렬의 1행 벡터가 뒤의 행렬의 두 열벡터 (1열, 2열)과 각각 내적이 이뤄지고, 이것이 결과로 나오는 행렬의
1행 1열 성분, 1행 2열 성분이 된다.
또한 앞의 행렬의 2행 벡터가 뒤의 행렬의 두 열벡터 (1열, 2열)과 각각 내적이 이뤄지고, 이것이 결과로 나오는 행렬의
2행 1열 성분, 2행 2열 성분이 된다.
(두 벡터의 내적값은 스칼라임을 기억하라)

그렇다면, 두 행렬의 곱셈을 앞의 행렬의 열벡터와 뒤의 행렬의 행벡터 연산 결과로 해석하는 방법은 없을까?
당연히 있다.
2. 벡터의 외적
열벡터와 행벡터의 곱셈은 행렬이 나온다고 하였다. (벡터의 외적, outer product)
그래서 앞의 행렬의 열벡터들과 뒤의 행렬의 행벡터를 외적해서 나오는 행렬들을 모두 더하면 행렬의 곱셈 연산이다.
역시나 2행 2열짜리 행렬 2개의 곱셈을 예시로 들면, 앞의 행렬의 1열 벡터와 뒤의 행렬의 1행 벡터, 앞의 행렬의 2열 벡터와 뒤의 행렬의 2행 벡터를 외적 연산을 수행하면 2개의 행렬이 나올 것이고 (2행 2열 크기) 그 두 행렬을 더하면 행렬의 곱셈 결과가 나온다.
행렬의 곱셈에서 중요한 성질이 또 있는데 첫 번째로 행렬의 곱셈이 항상 정의되지 않는다는 것과, 두 번째로 행렬의 곱셈은 교환법칙이 성립하지 않는다는 것이다.
행렬의 곱셈이 정의되기 위해서는 앞의 행렬의 열벡터 개수와 뒤의 행렬의 행벡터의 개수가 같아야 하는데, 앞의 행렬이 3행 2열이면, 뒤의 행렬은 행벡터가 무조건 2개인 행렬이어야 한다.
만약 뒤의 행렬이 행벡터가 2개가 아니라면, 행렬의 곱셈을 수행할 수 없다.
이를 일반화하여 표현하면 다음과 같다.

이러한 행렬 곱셈의 독특한 성질 덕분에 행렬 곱셈은 교환법칙이 성립하지 않는다.
만약 $m \times n$행렬과 $n \times p$행렬을 순서를 바꿔 곱한다면 어떻게 되겠는가? 곱셈 연산이 정의되지 않는다.
마지막으로, 그렇다면 행렬과 벡터를 곱셈하는 것도 가능할까?
당연히 가능하다.
행렬 ($A$)과 벡터 ($v$)의 곱셈을 우린 특별한 용어를 사용해서 부를 것이다. 바로 선형결합 (linear combination)이다.
정확히는 행렬의 열벡터의 '선형결합'이 곧 행렬과 벡터의 곱셈이다.
우선 행렬과 벡터의 곱셈을 계산하는 방법은 두 가지가 있다. 첫 번째는 행렬의 행벡터와 벡터의 내적이다.

행렬의 행벡터 $[1, 2, 3]$ 과 벡터 $[-1, -2, -3]$를 내적한 값은 $-14$이다.
또한, $[4,5,6]$과 벡터 $[-1, -2, -3]$를 내적한 값은 $-32$이다.

두 번째는 행렬의 열벡터의 선형결합으로 해석하는 것이다.
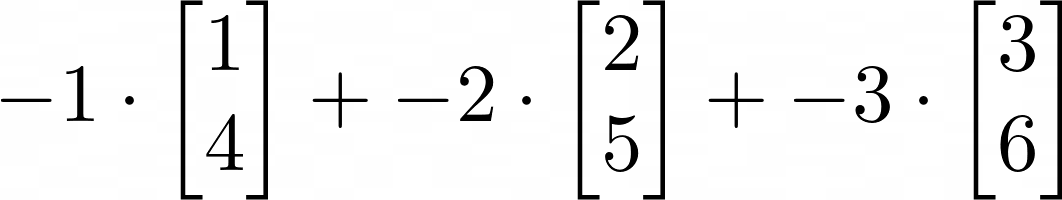
여기서 선형결합이란 무엇인지 정의하고 넘어가자.
벡터들의 선형결합은 다음과 같은 벡터들의 finite-sum을 의미한다.

여기서 $a_i$는 임의의 스칼라이고, $x_i$는 벡터이다.
연산의 결과는 당연히 벡터이고, 위 연산을 우리는 벡터 $x_i$들의 선형결합이라고 한다.
그리고 이러한 선형결합으로 만들어지는 모든 벡터들의 집합을 우리는 "span"이라 한다.
즉, 위와 같은 벡터 $\{x_1, x_2, \cdots, x_n\}$의 linear combination으로 표현되는 모든 벡터들의 집합은 $span(x_1, x_2, \cdots, x_n)$이다.
여기까지 벡터와 행렬의 정의 그리고 가장 기본적인 연산에 대해 알아보았다.
다음으로 특수한 행렬에 대해 알아보도록 하자.
1. 단위행렬 (Identity matrix, I)
단위행렬은 주 대각성분이 전부 1이고, 나머지는 전부 0인 행렬을 의미한다.
이 행렬은 행렬의 곱셈에서 일종의 '항등원' 역할을 하는데, 이는 어떤 행렬이든 단위행렬과의 곱셈은 자기 자신이라는 의미이다.
즉, 임의의 행렬 A에 대하여 $A I = I A = A$이다.

단위행렬은 무조건 행벡터의 개수와 열벡터의 개수가 같은 $R^{n \times n}$꼴이어야 한다.
2. 역행렬 (Inverse matrix, $A^{-1}$)
역행렬이란 곱셈에서 일종의 '역수'역할을 한다. 어떤 행렬과 곱했을 때, 단위행렬이 나오게 하는 행렬을 그 행렬의 역행렬이라 한다.
$A B = B A = I$이면 이때 $B$는 $A$ 행렬의 역행렬이다.
역행렬은 항상 존재하지 않으며, 역행렬이 존재하는 행렬을 가역행렬 , 비특이행렬이라고 부르고 역행렬이 존재하지 않는 행렬을 비가역행렬, 특이행렬이라고 부른다.
역행렬이 존재하기 위한 필요조건으로는 행렬의 행벡터와 열벡터의 개수가 같아야 한다는 것이 있다.
3. 대칭행렬 (Symmetry matrix)
대칭행렬이란 전치행렬이 자기 자신인 행렬을 말한다. ($A = A^T$)
즉, 그 행렬의 주 대각선을 기준으로 정확히 대칭인 행렬이다.
역시나 대칭행렬은 항상 행벡터와 열벡터의 개수가 같다. (당연한 사실이다.)

4. 직교행렬 (Orthogonal matrix)
직교행렬은 열벡터가 전부 직교인 행렬을 말한다.
그렇다면, 벡터가 직교인지는 어떻게 판단할까? 간단하다. 두 벡터를 내적해서 0이 나올 때 우리는 두 벡터가 직교한다고 한다.
즉, 이 말은 행렬의 열벡터들을 서로서로 내적했을 때, 전부 0이 나오는 행렬을 이야기한다.
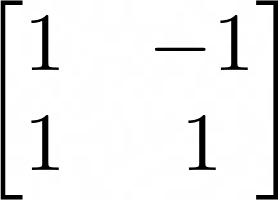
직교행렬은 매우 중요한 성질이 있는데 '직교행렬의 역행렬은 전치행렬이다.'
여기까지 기본적인 중요한 행렬에 대해서도 살펴보았다.
그렇다면 선형대수학에서 가장 중요한 방정식 2개를 알아보자.


두 번째 방정식은 다음 포스팅에서 정리할 것이고, 이번 포스팅에서는 첫 번째 방정식에 대한 기본적인 설명으로 마무리하겠다.
이때, $A \in \mathbb{R}^{m \times n}$, $x \in \mathvbb{R}^n$, $b \in \mathbb{R}^m$ 이라고 하자.
$m$과 $n$은 같을 수도 있고, 다를 수도 있다.
우선 $m = n$인 경우부터 살펴보자.
이처럼 행렬이 행벡터와 열벡터의 개수가 같은 경우를 우리는 정방 행렬 (Square Matrix)이라고 부른다.
자 위 방정식을 푼다는 것은 결국 위 방정식을 만족하는 solution $x$를 찾는 것이다.
가장 심플한 경우는 $A^{-1}$이 존재하는 경우이다.
양 변에 $A^{-1}$를 곱해주면, 결국 $x = A^{-1} b$가 된다. 유일한 해가 결정된다.
하지만, 문제는 역행렬이 항상 존재하지 않는 경우이다.
A가 정방행렬이어도 역행렬이 없을 수 있고, 정방행렬이 아니면 당연히 역행렬은 존재하지 않는다.
자, 그러면 이 경우에는 어떻게 될까?
크게 두 가지의 가능성이 존재한다. 첫 번째는 '해가 없는 경우'이다. (No solution)
그리고 두 번째는 '해가 무수히 많은 경우' 이다. (Infinitely many solutions)
잠시 어릴 때 배웠던 연립방정식을 떠올려보자.

미지수가 3개 ($x, y, z$)이고 방정식이 2개이다. 이 경우에는 해가 무수히 많이 있다.

미지수가 2개 ($x, y$)이고, 방정식이 3개이다. 이 경우에는 해가 없다.
자, 그런데 여기서 위 2개의 연립방정식을 우리는 $Ax = b$ 꼴로 표현할 수 있다.

정확히 첫 번째 연립방정식과 동치의 방정식이다.
이때 행렬 $A$를 보면, $A$는 행벡터가 2개, 열벡터가 3개이다. ($\mathbb{R}^{2 \times 3}$)
이 경우는 식의 개수보다 미지수의 개수가 많기 때문에 해가 무수히 많이 있다.

정확히 두 번째 연립방정식과 동치의 방정식이다.
이때 행렬 $A$는 행벡터가 3개, 열벡터가 2개이다. ($\mathbb{R}^{3 \times 2}$)
이 경우는 미지수의 개수보다 식의 개수가 많기 때문에 해가 없다.
그렇다면, 우리한테 드는 의문점은 크게 두 가지이다.
* 역행렬이 존재할 때만 해가 $x = A^{-1}b$로 유일하게 결정된다고 하였다.
그렇다면 언제 역행렬이 존재하는 것일까?
* 그리고 해가 없는 경우, 정말 우리는 해가 없다라고 결론을 내리는 것이 최선일까?
최대한 괜찮은 해라도 구할 수 있는 방법이 없을까?
수학적으로 표현하면, '근사해' (approximated solution)이라도 구할 수 있는 방법이 없을까?
이 두 가지도 선형대수학에서 매우 중요한 개념이고 이를 이해하기 위해서는 우선 선형독립, 선형종속의 개념을 알아야 한다.
다음 글에서 위 두 가지의 질문에 대한 답을 설명해나가고, $Ax = \lambda x$에 대해 설명하고 선형대수학 포스팅을 마무리하겠다.
'Deep dive into Deep learning' 카테고리의 다른 글
| Deep dive into Deep learning part 6. - Updated (0) | 2023.03.17 |
|---|---|
| Deep dive into Deep learning part 5. - Updated (1) | 2023.03.13 |
| Deep dive into Deep Learning Part 4. - Updated (0) | 2023.03.09 |
| Deep dive into deep learning part 2. - Updated (0) | 2023.03.05 |
| Deep Learning part 1. 딥러닝과 머신러닝 (Updated) (0) | 2023.03.04 |




댓글